Bill of material based on characteristics
The composition of a product can be represented using a directed acyclic graph, called real structure, in which every node is an aggregation of its children nodes:
- The end nodes are individual components
- The intermediate nodes are partial assemblies
- The root node is the final product
The graph arcs show the quantities of child components required to create a single instance of the parent, whether the parent is a partial assembly or the final product. The graph representation can be more useful than a tree representation in cases where the same component type is used repeatedly in building different assemblies.
This graph type can also be applied to a production process, in which case it is known as an ideal structure graph, in which each node represents a process step:
- The leaves of the graph correspond to a single step of the production process
- The intermediate nodes represent a macro phase or a next step
- The root of the graph represents the entire process.
 Real structure Y3 = 1*X4 + 1*Y2, Y2 = 1*X3 + 2*Y1, Y1 = 3*X1 + 1*X2 |
 Ideal structure Production steps sequence:: A, B, C |
It is possible to create a single structure that contains both the ideal (production steps), and the real one (components, assemblies), called technological structure: to the nodes of the ideal structure, known as idealnodes, there are links to the nodes of the real structure, called real nodes, used in the production step mapped by the ideal node. If the considered ideal node is a leaf of the ideal structure, it is linked to the entire real subgraph that expresses the composition of the real node used in its production step; otherwise it binds only the single real node used, while his components are linked to the ideal nodes of the subgraph which describes the production steps. On the arcs of the graph that connect a real node to an ideal node is indicated the quantity of the real node used in the ideal node mapped production step.

Use of characteristics to configurate the Bill Of Material (BOM) Structure
The product variations can be expressed using characteristics (or features): every product variation is defined by a combination of these characteristic values. If the considered product can have several variations, it can be too expensive to define each one of these with a different BOM structure. Using the technological structure and the characteristics, it is possible to define all the product variations in a single BOM structure simultaneously. It is sufficient to assign to the link between a real node and an ideal node, a characteristics based boolean function, which we shall term the application function. The value of this function will be true only when the combination of the characteristic values corresponds to a product variation where the real node is used effectively.
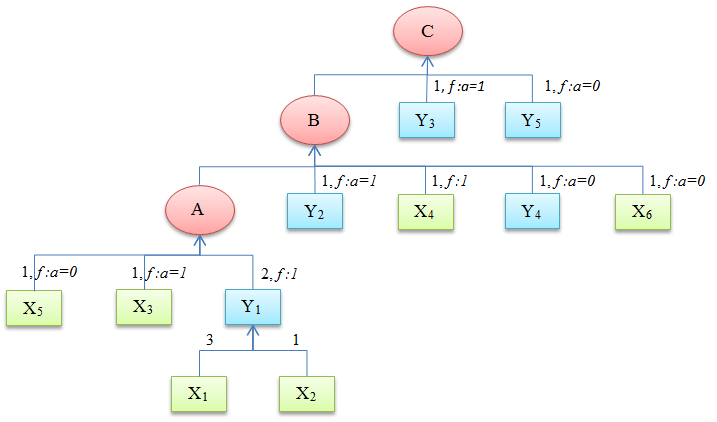
BOM structure navigation
Given a product variation, represented by a specific characteristics valorization, it is possible to dynamically obtain the BOM structure navigating the technological structure and selecting only the real nodes having a true application function. Furthermore, linking each selected assembly with the real nodes selected in his sub graph it is possible to dynamically build also the real structure.
It is similarly possible to obtain the composition of an assembly related to an ideal node: it is sufficient to visit the sub-graph having as root the ideal node itself, excluding the starting real node siblings, and selecting the real nodes which application function has a not empty intersection with the application function of the starting real node (i.e. it exists a characteristic values combination where the two functions are both true ).
It is moreover possible, given a real node, to obtain all the assemblies it can belong to; if it belongs to a real structure, it navigates the structure in bottom-up direction: all the encountered real nodes are composed by the starting real node. Then, for each encounterd real node linked to an ideal node, it traces the application function f and visit in bottom-up direction the ideal structure: for each parent ideal node, all the real node related to it and having a not empty application function intersection with f (i.e. it exists a characteristic values combination where the two functions are both true ) are then composed by the starting real node.

References
- Yatna Yuwana Martawirya, Sri Raharno and Indra Nurhadi. "Development of Bill of Materials of Product Variants". http://www.knu.edu.tw/lecture/%E6%AD%B7%E5%B9%B4%E6%95%99%E5%AD%B8%E8%B3%87%E6%96%99/2008%20APIEMS(BALI)/PAPER/351-Yatna%20Yuwana%20Martawirya.pdf
- Jianxin Jiao, Mitchell M. Tseng, Qinhai Ma and Yi Zou. 2000. "Generic Bill-of-Materials-and-Operations for High-Variety Production Management" Concurrent Engineering:Research and applications [297-321]. http://ami.ust.hk/Archived%20Journals/Generic%20Bill-of-Materials-and-Operations%20for%20High-Variety%20Production%20Management.pdf