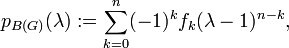Bicircular matroid

In the mathematical subject of matroid theory, the bicircular matroid of a graph G is the matroid B(G) whose points are the edges of G and whose independent sets are the edge sets of pseudoforests of G, that is, the edge sets in which each connected component contains at most one cycle.

The bicircular matroid was introduced by Simões-Pereira (1972) and explored further by Matthews (1977) and others. It is a special case of the frame matroid of a biased graph.

Circuits

The circuits, or minimal dependent sets, of this matroid are the bicircular graphs (or bicycles, but that term has other meanings in graph theory); these are connected graphs whose circuit rank is exactly two.

There are three distinct types of bicircular graph:

All these definitions apply to multigraphs, i.e., they permit multiple edges (edges sharing the same endpoints) and loops (edges whose two endpoints are the same vertex).

Flats

The closed sets (flats) of the bicircular matroid of a graph G can be described as the forests F of G such that in the induced subgraph of V(G) − V(F), every connected component has a cycle. Since the flats of a matroid form a geometric lattice when partially ordered by set inclusion, these forests of G also form a geometric lattice. In the partial ordering for this lattice, that F1 ≤ F2 if

For the most interesting example, let G o be G with a loop added to every vertex. Then the flats of B(G o) are all the forests of G, spanning or nonspanning. Thus, all forests of a graph G form a geometric lattice, the forest lattice of G (Zaslavsky 1982).

As transversal matroids

Bicircular matroids can be characterized as the transversal matroids that arise from a family of sets in which each set element belongs to at most two sets. That is, the independent sets of the matroid are the subsets of elements that can be used to form a system of distinct representatives for some or all of the sets. In this description, the elements correspond to the edges of a graph, and there is one set per vertex, the set of edges having that vertex as an endpoint.

Minors

Unlike transversal matroids in general, bicircular matroids form a minor-closed class; that is, any submatroid or contraction of a bicircular matroid is also a bicircular matroid, as can be seen from their description in terms of biased graphs (Zaslavsky 1991). Here is a description of deletion and contraction of an edge in terms of the underlying graph: To delete an edge from the matroid, remove it from the graph. The rule for contraction depends on what kind of edge it is. To contract a link (a non-loop) in the matroid, contract it in the graph in the usual way. To contract a loop e at vertex v, delete e and v but not the other edges incident with v; rather, each edge incident with v and another vertex w becomes a loop at w. Any other graph loops at v become matroid loops—to describe this correctly in terms of the graph one needs half-edges and loose edges; see biased graph minors.

Characteristic polynomial

The characteristic polynomial of the bicircular matroid B(G o) expresses in a simple way the numbers of spanning forests (forests that contain all vertices of G) of each size in G. The formula is

p_{B(G)}(\lambda) := \sum_{k=0}^n (-1)^k f_k (\lambda-1)^{n-k},

where fk equals the number of k-edge spanning forests in G. See Zaslavsky (1982).

Vector representation

Bicircular matroids, like all other transversal matroids, can be represented by vectors over any infinite field. However, unlike graphic matroids, they are not regular: they cannot be represented by vectors over an arbitrary finite field. The question of the fields over which a bicircular matroid has a vector representation leads to the largely unsolved problem of finding the fields over which a graph has multiplicative gains. See Zaslavsky (2007).

References

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.