Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of Lie algebras.
The system classifies 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes. (Sometimes two of the groups are included in the infinite families, giving 9 instead of 11 classes.)
Cosmological application
In cosmology, this classification is used for a homogeneous spacetime of dimension 3+1. The Friedmann–Lemaître–Robertson–Walker metrics are isotropic, which are particular cases of types I, V, 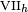 and IX. The Bianchi type I models include the Kasner metric as a special case.
The Bianchi IX cosmologies include the Taub metric.[1] However, the dynamics near the singularity is approximately governed by a series of successive Kasner (Bianchi I) periods. The complicated dynamics,
which essentially amounts to billiard motion in a portion of hyperbolic space, exhibits chaotic behaviour, and is named Mixmaster; its analysis is referred to as the BKL analysis after Belinskii, Khalatnikov and Lifshitz.
[2]
[3]
More recent work has established a relation of (super-)gravity theories near a spacelike singularity (BKL-limit) with Lorentzian Kac–Moody algebras, Weyl groups and hyperbolic Coxeter groups.[4][5][6]
Other more recent work is concerned with the discrete nature of the Kasner map and a continuous generalisation.[7][8][9]
and IX. The Bianchi type I models include the Kasner metric as a special case.
The Bianchi IX cosmologies include the Taub metric.[1] However, the dynamics near the singularity is approximately governed by a series of successive Kasner (Bianchi I) periods. The complicated dynamics,
which essentially amounts to billiard motion in a portion of hyperbolic space, exhibits chaotic behaviour, and is named Mixmaster; its analysis is referred to as the BKL analysis after Belinskii, Khalatnikov and Lifshitz.
[2]
[3]
More recent work has established a relation of (super-)gravity theories near a spacelike singularity (BKL-limit) with Lorentzian Kac–Moody algebras, Weyl groups and hyperbolic Coxeter groups.[4][5][6]
Other more recent work is concerned with the discrete nature of the Kasner map and a continuous generalisation.[7][8][9]
Classification
Lower Dimensions
In zero dimensions, the only Lie algebra is the abelian Lie algebra R0. In one dimension, the only Lie algebra is the abelian Lie algebra R1, with outer automorphism group the group of non-zero real numbers.
In two dimentions, there are two Lie algebras:
- The abelian Lie algebra R2, with outer automorphism group GL2(R).
- The solvable Lie algebra of 2×2 upper triangular matrices of trace 0. The simply connected group has trivial center and outer automorphism group of order 2; it is the affine group of the line.
Dimension 3
All the 3-dimensional Lie algebras other than types VIII and IX can be constructed as a semidirect product of R2 and R, with R acting on R2 by some 2 by 2 matrix M. The different types correspond to different types of matrices M, as described below.
- Type I: This is the abelian and unimodular Lie algebra R3. The simply connected group has center R3 and outer automorphism group GL3(R). This is the case when M is 0.
- Type II: Nilpotent and unimodular: Heisenberg algebra. The simply connected group has center R and outer automorphism group GL2(R). This is the case when M is nilpotent but not 0 (eigenvalues all 0).
- Type III: Solvable and not unimodular. This algebra is a product of R and the 2-dimensional non-abelian Lie algebra. (It is a limiting case of type VI, where one eigenvalue becomes zero.) The simply connected group has center R and outer automorphism group the group of non-zero real numbers. The matrix M has one zero and one non-zero eigenvalue.
- Type IV: Solvable and not unimodular. [y,z] = 0, [x,y] = y, [x, z] = y + z. The simply connected group has trivial center and outer automorphism group the product of the reals and a group of order 2. The matrix M has two equal non-zero eigenvalues, but is not semisimple.
- Type V: Solvable and not unimodular. [y,z] = 0, [x,y] = y, [x, z] = z. (A limiting case of type VI where both eigenvalues are equal.) The simply connected group has trivial center and outer automorphism group the elements of GL2(R) of determinant +1 or −1. The matrix M has two equal eigenvalues, and is semisimple.
- Type VI: Solvable and not unimodular. An infinite family. Semidirect products of R2 by R, where the matrix M has non-zero distinct real eigenvalues with non-zero sum. The simply connected group has trivial center and outer automorphism group a product of the non-zero real numbers and a group of order 2.
- Type VI0: Solvable and unimodular. This Lie algebra is the semidirect product of R2 by R, with R where the matrix M has non-zero distinct real eigenvalues with zero sum. It is the Lie algebra of the 2-dimensional Poincaré group, the group of isometries of 2-dimensional Minkowski space. The simply connected group has trivial center and outer automorphism group the product of the positive real numbers with the dihedral group of order 8.
- Type VII: Solvable and not unimodular. An infinite family. Semidirect products of R2 by R, where the matrix M has non-real and non-imaginary eigenvalues. The simply connected group has trivial center and outer automorphism group the non-zero reals.
- Type VII0: Solvable and unimodular. Semidirect products of R2 by R, where the matrix M has non-zero imaginary eigenvalues. This is the Lie algebra of the group of isometries of the plane. The simply connected group has center Z and outer automorphism group a product of the non-zero real numbers and a group of order 2.
- Type VIII: Semisimple and unimodular. The Lie algebra sl2(R) of traceless 2 by 2 matrices. The simply connected group has center Z and its outer automorphism group has order 2.
- Type IX: Semisimple and unimodular. The Lie algebra of the orthogonal group O3(R). The simply connected group has center of order 2 and trivial outer automorphism group, and is a spin group.
The classification of 3-dimensional complex Lie algebras is similar except that types VIII and IX become isomorphic, and types VI and VII both become part of a single family of Lie algebras.
The connected 3-dimensional Lie groups can be classified as follows: they are a quotient of the corresponding simply connected Lie group by a discrete subgroup of the center, so can be read off from the table above.
The groups are related to the 8 geometries of Thurston's geometrization conjecture. More precisely, seven of the 8 geometries can be realized as a left-invariant metric on the simply connected group (sometimes in more than one way). The Thurston geometry of type S2×R cannot be realized in this way.
Structure constants
The three-dimensional Bianchi spaces each admit a set of three Killing vectors 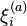 which obey the following property:
which obey the following property:
where 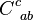 , the "structure constants" of the group, form a constant order-three tensor antisymmetric in its lower two indices. For any three-dimensional Bianchi space,
, the "structure constants" of the group, form a constant order-three tensor antisymmetric in its lower two indices. For any three-dimensional Bianchi space, 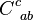 is given by the relationship
is given by the relationship
where 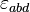 is the Levi-Civita symbol,
is the Levi-Civita symbol, 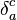 is the Kronecker delta, and the vector
is the Kronecker delta, and the vector 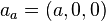 and diagonal tensor
and diagonal tensor 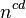 are described by the following table, where
are described by the following table, where 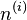 gives the ith eigenvalue of
gives the ith eigenvalue of 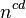 ;[10] the parameter a runs over all positive real numbers:
;[10] the parameter a runs over all positive real numbers:
| Bianchi type |  |
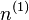 |
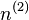 |
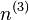 |
notes |
|---|---|---|---|---|---|
| I | 0 | 0 | 0 | 0 | describes Euclidean space |
| II | 0 | 1 | 0 | 0 | |
| III | 1 | 0 | 1 | -1 | the subcase of type VIa with  |
| IV | 1 | 0 | 0 | 1 | |
| V | 1 | 0 | 0 | 0 | has a hyper-pseudosphere as a special case |
| VI0 | 0 | 1 | -1 | 0 | |
| VIa |  | 0 | 1 | -1 | when  , equivalent to type III , equivalent to type III |
| VII0 | 0 | 1 | 1 | 0 | has Euclidean space as a special case |
| VIIa |  | 0 | 1 | 1 | has a hyper-pseudosphere as a special case |
| VIII | 0 | 1 | 1 | -1 | |
| IX | 0 | 1 | 1 | 1 | has a hypersphere as a special case |
Curvature of Bianchi spaces
The Bianchi spaces have the property that their Ricci tensors can be separated into a product of the basis vectors associated with the space and a coordinate-independent tensor.
For a given metric
(where 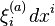 are 1-forms), the Ricci curvature tensor
are 1-forms), the Ricci curvature tensor  is given by:
is given by:
where the indices on the structure constants are raised and lowered with 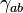 which is not a function of
which is not a function of 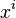 .
.
See also
References
- ↑ Robert Wald, General Relativity, University of Chicago Press (1984). ISBN 0-226-87033-2, (chapt 7.2, pages 168–179)
- ↑ V. A. Belinskii, I. M. Khalatnikov, and E. M. Lifshitz, Zh. Eksp. Teor. Fiz. 62, 1606 (1972)
- ↑ V. A. Belinskii, I. M. Khalatnikov, and E. M. Lifshitz, Zh. Eksp. Teor. Fiz. 60, 1969 (1971)
- ↑ M. Henneaux, D. Persson, and P. Spindel, Living Reviews in Relativity 11, 1 (2008), 0710.1818
- ↑ M. Henneaux, D. Persson, and D. H. Wesley, Journal of High Energy Physics 2008, 052 (2008)
- ↑ M. Henneaux, ArXiv e-prints (2008), 0806.4670
- ↑ N. J. Cornish and J. J. Levin, in Recent Developments in Theoretical and Experimental General Relativity, Gravitation, and Relativistic Field Theories, edited by T. Piran and R. Ruffini (1999), pp. 616–+
- ↑ N. J. Cornish and J. J. Levin, Phys. Rev. Lett. 78, 998 (1997)
- ↑ N. J. Cornish and J. J. Levin, Phys. Rev. D 55, 7489 (1997)
- ↑ Lev Landau and Evgeny Lifshitz (1980), Course of Theoretical Physics vol. 2: The Classical Theory of Fields, Butterworth-Heinemann, ISBN 978-0-7506-2768-9
- L. Bianchi, Sugli spazii a tre dimensioni che ammettono un gruppo continuo di movimenti. (On the spaces of three dimensions that admit a continuous group of movements.) Soc. Ital. Sci. Mem. di Mat. 11, 267 (1898) English translation
- Guido Fubini Sugli spazi a quattro dimensioni che ammettono un gruppo continuo di movimenti, (On the spaces of four dimensions that admit a continuous group of movements.) Ann. Mat. pura appli. (3) 9, 33-90 (1904); reprinted in Opere Scelte, a cura dell'Unione matematica italiana e col contributo del Consiglio nazionale delle ricerche, Roma Edizioni Cremonese, 1957–62
- MacCallum, On the classification of the real four-dimensional Lie algebras, in "On Einstein's path: essays in honor of Engelbert Schucking" edited by A. L. Harvey, Springer ISBN 0-387-98564-6
- Robert T. Jantzen, Bianchi classification of 3-geometries: original papers in translation
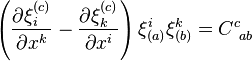
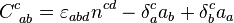
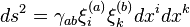
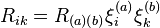
![R_{(a)(b)} = \frac{1}{2} \left[ C^{cd}_{\ \ b} \left( C_{cda} + C_{dca} \right) + C^c_{\ cd} \left( C^{\ \ d}_{ab} + C^{\ \ d}_{ba} \right) - \frac{1}{2} C^{\ cd}_b C_{acd} \right]](../I/m/906636ffa0445d875f53766f9ad503fc.png)