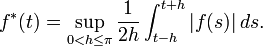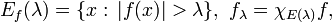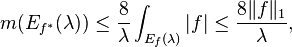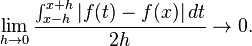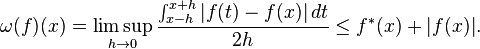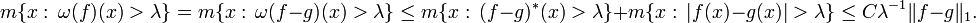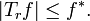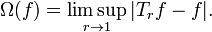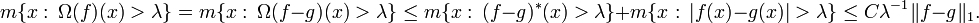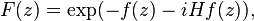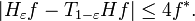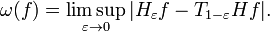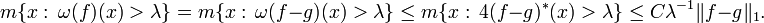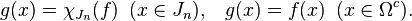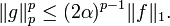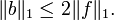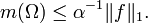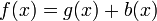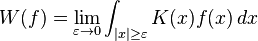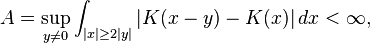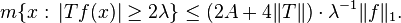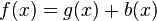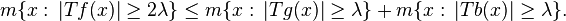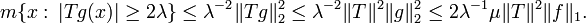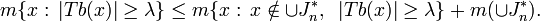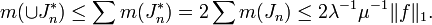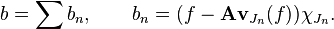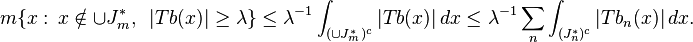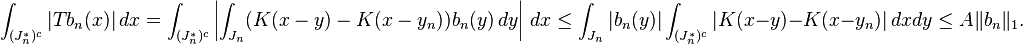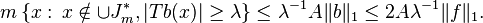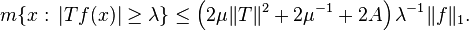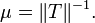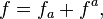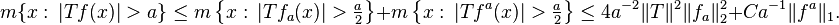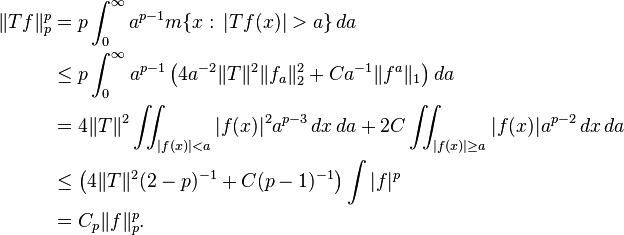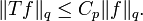Singular integral operators of convolution type
In mathematics, singular integral operators of convolution type are the singular integral operators that arise on Rn and Tn through convolution by distributions; equivalently they are the singular integral operators that commute with translations. The classical examples in harmonic analysis are the harmonic conjugation operator on the circle, the Hilbert transform on the circle and the real line, the Beurling transform in the complex plane and the Riesz transforms in Euclidean space. The continuity of these operators on L2 is evident because the Fourier transform converts them into multiplication operators. Continuity on Lp spaces was first established by Marcel Riesz. The classical techniques include the use of Poisson integrals, interpolation theory and the Hardy–Littlewood maximal function. For more general operators, fundamental new techniques, introduced by Alberto Calderón and Antoni Zygmund in 1952, were developed by a number of authors to give general criteria for continuity on Lp spaces. This article explains the theory for the classical operators and sketches the subsequent general theory.
L2 theory
Hilbert transform on the circle
The theory for L2 functions is particularly simple on the circle.[1][2] If f ∈ L2(T), then it has a Fourier series expansion
Hardy space H2(T) consists of the functions for which the negative coefficients vanish, an = 0 for n < 0. These are precisely the square-integrable functions that arise as boundary values of holomorphic functions in the open unit disk. Indeed, f is the boundary value of the function
in the sense that the functions
defined by the restriction of F to the concentric circles |z| = r, satisfy
The orthogonal projection P of L2(T) onto H2(T) is called the Szegő projection. It is a bounded operator on L2(T) with operator norm 1. By Cauchy's theorem
Thus
When r = 1, the integrand on the right hand side has a singularity at θ = 0. The truncated Hilbert transform is defined by
where δ = |1 – eiε|. Since it is defined as convolution with a bounded function, it is a bounded operator on L2(T). Now
If f is a polynomial in z then
By Cauchy's theorem the right hand side tends to 0 uniformly as ε, and hence δ, tends to 0. So
uniformly for polynomials. On the other hand, if u(z) = z it is immediate that
Thus if f is a polynomial in z−1 without constant term
 uniformly.
uniformly.
Define the Hilbert transform on the circle by
Thus if f is a trigonometric polynomial
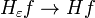 uniformly.
uniformly.
It follows that if f is any L2 function
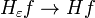 in the L2 norm.
in the L2 norm.
This is an immediate consequence of the result for trigonometric polynomials once it is established that the operators Hε are uniformly bounded in operator norm. But on [–π,π]
The first term is bounded on the whole of [–π,π], so it suffices to show that the convolution operators Sε defined by
are uniformly bounded. With respect to the orthonormal basis einθ convolution operators are diagonal and their operator norms are given by taking the supremum of the moduli of the Fourier coefficients. Direct computation shows that these all have the form
with 0 < a < b. These integrals are well-known to be uniformly bounded.
It also follows that, for a continuous function f on the circle, Hεf converges uniformly to Hf, so in particular pointwise. The pointwise limit is a Cauchy principal value, written
If f is just in L2 then Hεf converges to Hf pointwise almost everywhere. In fact define the Poisson operators on L2 functions by
for r < 1. Since these operators are diagonal, it is easy to see that Trf tends to f in L2 as r increases to 1. Moreover, as Lebesgue proved, Trf also tends pointwise to f at each Lebesgue point of f. On the other hand, it is also known that TrHf – H1 – r f tends to zero at each Lebesgue point of f. Hence H1 – r f tends pointwise to f on the common Lebesgue points of f and Hf and therefore almost everywhere.[3][4][5]
Results of this kind on pointwise convergence are proved more generally below for Lp functions using the Poisson operators and the Hardy–Littlewood maximal function of f.
The Hilbert transform has a natural compatibility with orientation-preserving diffeomorphisms of the circle.[6] Thus if H is a diffeomorphism of the circle with
then the operators
are uniformly bounded and tend in the strong operator topology to H. Morevoer if Vf(z) = f(H(z)), then VHV−1 – H is an operator with smooth kernel, so a Hilbert–Schmidt operator.
In fact if G is the inverse of H with corresponding function g(θ), then
Since the kernel on the right hand side is smooth on T × T, it follows that the operators on the right hand side are uniformly bounded and hence so too are the operators Hεh. To see that they tend strongly to H, it suffices to check this on trigonometric polynomials. In that case
In the first integral the integrand is a trigonometric polynomial in z and ζ and so the integral is a trigonometric polynomial in ζ. It tends in L2 to the trigonometric polynomial
The integral in the second term can be calculated by the principle of the argument. It tends in L2 to the constant function 1, so that
where the limit is in L2. On the other hand, the right hand side is imdependent of the diffeomorphism. Since for the identity diffeomorphism, the left hand side equals Hf, it too equals Hf (this can also be checked directly if f is a trigonometric polynomial). Finally, letting ε → 0,
The direct method of evaluating Fourier coefficients to prove the uniform boundedness of the operator Hε does not generalize directly to Lp spaces with 1 < p < ∞. Instead a direct comparison of Hεf with the Poisson integral of the Hilbert transform is used classically to prove this. If f has Fourier series
its Poisson integral is defined by
where the Poisson kernel Kr is given by
In f is in Lp(T) then the operators Pr satisfy
In fact the Kr are positive so
Thus the operators Pr have operator norm bounded by 1 on Lp. The convergence statement above follows by continuity from the result for trigonometric polynomials, where it is an immediate consequence of the formula for the Fourier coefficients of Kr.
The uniform boundedness of the operator norm of Hε follows because HPr − H1−r is given as convolution by the function ψr, where[7]
for 1 − r ≤ |θ| ≤ π, and, for |θ| < 1 − r,
These estimates show that the L1 norms ∫ |ψr| are uniformly bounded. Since H is a bounded operator, it follows that the operators Hε are uniformly bounded in operator norm on L2(T). The same argument can be used on Lp(T) once it is known that that the Hilbert transform H is bounded in operator norm on Lp(T).
Hilbert transform on the real line
As in the case of the circle, the theory for L2 functions is particularly easy to develop. In fact, as observed by Rosenblum and Devinatz, the two Hilbert transforms can be related using the Cayley transform.[8]
The Hilbert transform HR on L2(R) is defined by
where the Fourier transform is given by
Define the Hardy space H2(R) to be the closed subspace of L2(R) consisting of functions for which the Fourier transform vanishes on the negative part of the real axis. Its orthogonal complement is given by functions for which the Fourier transform vanishes on the positive part of the real axis. It is the complex conjugate of H2(R). If PR is the orthogonal projection onto H2(R), then
The Cayley transform
carries the extended real line onto the circle, sending the point at ∞ to 1, and the upper halfplane onto the unit disk.
Define the unitary operator from L2(T) onto L2(R) by
This operator carries the Hardy space of the circle H2(T) onto H2(R). In fact for |w| < 1, the linear span of the functions
is dense in H2(T). Moreover,
where
On the other hand, for z ∈ H, the linear span of the functions
is dense in L2((0,∞)). By the Fourier inversion formula, they are the Fourier transforms of
so the linear span of these functions is dense in H2(R). Since U carries the fw's onto multiples of the hz's, it follows that U carries H2(T) onto H2(R). Thus
In Nikolski (1986), part of the L2 theory on the real line and the upper halfplane is developed by transferring the results from the circle and the unit disk. The natural replacements for concentric circles in the disk are lines parallel to the real axis in H. Under the Cayley transform these correspond to circles in the disk that are tangent to the unit circle at the point one. The behaviour of functions in H2(T) on these circles is part of the theory of Carleson measures. The theory of singular integrals, however, can be developed more easily by working directly on R.
H2(R) consists exactly of L2 functions f that arise of boundary values of holomorphic functions on H in the following sense:[9] f is in H2 provided that there is a holomorphic function F(z) on H such that the functions fy(x) = f(x + iy) for y > 0 are in L2 and fy tends to f in L2 as y → 0. In this case F is necessarily unique and given by Cauchy's integral formula:
In fact, identifying H2 with L2(0,∞) via the Fourier transform, for y > 0 multiplication by e−yt on L2(0,∞) induces a contraction semigroup Vy on H2. Hence for f in L2
If f is in H2, F(z) is holomorphic for Im z > 0, since the family of L2 functions gz depends holomorphically on z. Moreover, fy = Vyf tends to f in H2 since this is true for the Fourier transforms. Conversely if such an F exists, by Cauchy's integral theorem and the above identity applied to fy
for t > 0. Letting t tend to 0, it follows that Pfy = fy, so that fy lies in H2. But then so too does the limit f. Since
uniqueness of F follows from
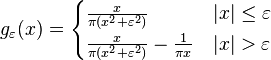
For f in L2, the truncated Hilbert transforms are defined by
The operators Hε,R are convolutions by bounded functions of compact support, so their operator norms are given by the uniform norm of their Fourier transforms. As before the absolute values have the form
with 0 < a < b, so the operators Hε,R are uniformly bounded in operator norm. Since Hε,Rf tends to Hεf in L2 for f with compact support, and hence for arbitrary f, the operators Hε are also uniformly bounded in operator norm.
To prove that Hε f tends to Hf as ε tends to zero, it suffices to check this on a dense set of functions. On the other hand,
so it suffices to prove that Hεf tends to if for a dense set of functions in H2(R), for example the Fourier transforms of smooth functions g with compact support in (0,∞). But the Fourier transform f extends to an entire function F on C, which is bounded on Im(z) ≥ 0. The same is true of the derivatives of g. Up to a scalar these correspond to multiplying F(z) by powers of z. Thus F satisfies a Payley-Wiener estimate for Im(z) ≥ 0:[10]
for any m, N ≥ 0. In particular, the integral defining Hεf(x) can be computed by taking a standard semicircle contour centered on x. It consists of a large semicircle with radius R and a small circle radius ε with the two portions of the real axis between them. By Cauchy's theorem, the integral round the contour is zero. The integral round the large contour tends to zero by the Paley-Wiener estimate. The integral on the real axis is the limit sought. It is therefore given as minus the limit on the small semicircular contour. But this is the limit of
Where Γ is the small semicircular contour, oriented anticlockwise. By the usual techniques of contour integration, this limit equals if(x).[11] In this case, it is easy to check that the convergence is dominated in L2 since
so that convergence is dominated by
which is in L2 by the Paley-Wiener estimate.
It follows that for f on L2(R)
This can also be deduced directly because, after passing to Fourier transforms, Hε and H become multiplication operators by uniformly bounded functions. The multipliers for Hε tend pointwise almost everywhere to the multiplier for H, so the statement above follows from the dominated convergence theorem applied to the Fourier transforms.
As for the Hilbert transform on the circle, Hεf tends to Hf pointwise almost everywhere if f is an L2 function. In fact, define the Poisson operators on L2 functions by
where the Poisson kernel is given by
for y > 0. Its Fourier transform is
from which it is easy to see that Tyf tends to f in L2 as y increases to 0. Moreover, as Lebesgue proved, Tyf also tends pointwise to f at each Lebesgue point of f. On the other hand, it is also known that TyHf – Hyf tends to zero at each Lebesgue point of f. Hence Hεf tends pointwise to f on the common Lebesgue points of f and Hf and therefore almost everywhere.[12][13] The absolute values of the functions Tyf − f and TyHf – Hyf can be bounded pointwise by multiples of the maximal function of f.[14]
As for the Hilbert transform on the circle, the uniform boundedness of the operator norms of Hε follows from that of the Tε if H is known to be bounded, since HTε − Hε is the convolution operator by the function
The L1 norms of these functions are uniformly bounded.
Riesz transforms in the complex plane
The complex Riesz transforms R and R* in the complex plane are the unitary operators on L2(C) defined as multiplication by z/|z| and its conjugate on the Fourier transform of an L2 function f:
Idenitifying C with R2, R and R* are given by
where R1 and R2 are the Riesz transforms on R2 defined below.
On L2(C), the operator R and its integer powers are unitary. They can also be expressed as singular integral operators:[15]
where
Defining the truncated higher Riesz transforms as
these operators can be shown to be uniformly bounded in operator norm. For odd powers this can be deduced by the method of rotation of Calderón and Zygmund, described below.[16] If the operators are known to be bounded in operator norm it can also be deduced using the Poisson operators.[17]
The Poisson operators Ts on R2 are defined for s > 0 by
They are given by convolution with the functions
Ps is the Fourier transform of the function e− s|x|, so under the Fourier transform they correspond to multiplication by these functions and form a contraction semigroup on L2(R2). Since Py is positive and integrable with integral 1, the operators Ts also define a contraction semigroup on each Lp space with 1 < p < ∞.
The higher Riesz transforms of the Poisson kernel can be computed:
for k ≥ 1 and the complex conjugate for − k. Indeed, the right hand side is a harmonic function F(x,y,s) of three variable and for such functions[18]
As before the operators
are given by convolution with integrable functions and have uniformly bounded operator norms. Since the Riesz transforms are unitary on L2(C), the uniform boundedness of the truncated Riesz transforms implies that they converge in the strong operator topology to the corresponding Riesz transforms.
The uniform boundedness of the difference between the transform and the truncated transform can also be seen for odd k using the Calderón-Zygmund method of rotation.[19][20] The group T acts by rotation on functions on C via
This defines a unitary representation on L2(C) and the unitary operators Rθ commute with the Fourier transform. If A is a bounded operator on L2(R) then it defines a bounded operator A(1) on L2(C) simply by making A act on the first coordinate. With the identification L2(R2) = L2(R) ⊗ L2(R), A(1) = A ⊗ I. If φ is a continuous function on the circle then a new operator can be defined by
This definition is understood in the sense that
for any f, g in L2(C). It follows that
Taking A to be the Hilbert transform H on L2(R) or its truncation Hε, it follows that
Taking adjoints gives a similar formuls for R* and its truncation. This gives a second way to verify estimate the norms of R, R* and their truncations. It has the advantage of being applicable also for Lp spaces.
The Poisson operators can also be used to show that the truncated higher Riesz transforms of a function tend to the higher Riesz transform at the common Lebesgue points of the function and its transform. Indeed, (RkTε − R(k)ε)f → 0 at each Lebesgue point of f; while (Rk − RkTε)f → 0 at each Lebesgue point of Rkf.[21]
Beurling transform in the complex plane
Since
the Beurling transform T on L2 is the unitary operator equal to R2. This relation has been used classically in Vekua (1962) and Ahlfors (1966) to establish the continuity properties of T on Lp spaces. The results on the Riesz transform and its powers show that T is the limit in the strong operator topology of the truncated operators
Accordingly, Tf can be written as a Cauchy principal value integral:
From the description of T and T* on Fourier transforms, it follows that if f is smooth of compact support
Like the Hilbert transform in one dimension, the Beurling transform has a compatibility with conformal changes of coordinate. Let Ω be a bounded region in C with smooth boundary ∂Ω and let φ be a univalent holomorphic map of the unit disk D onto Ω extending to a smooth diffeomorphism of the circle onto ∂Ω. If χΩ is the characteristic function of Ω, the operator can χΩTχΩ defines an operaror T(Ω) on L2(Ω). Through the conformal map φ, it induces an operator, also denoted T(Ω), on L2(D) which can be compared with T(D). The same is true of the truncations Tε(Ω) and Tε(D).
Let Uε be the disk |z − w| < ε and Vε the region |φ(z) − φ(w)| < ε. On L2(D)
and the operator norms of these truncated operators are uniformly bounded. On the other hand, if
then the difference between this operator and Tε(Ω) is a truncated operator with smooth kernel K(w,z):
So the operators T′ε(D) must also have uniformly bounded operator norms. To see that their difference tends to 0 in the strong operator topology, it is enough to check this for f smooth of compact support in D. By Green's theorem[22]
All four terms on the right hand side tend to 0. Hence the difference T(Ω) − T(D) is the Hilbert–Schmidt operator with kernel K.
For pointwise convergence there is simple argument due to Mateu & Verdera (2006) showing that the truncated integrals converge to Tf precisely at its Lebesgue points, that is almost everywhere.[23] In fact T has the following symmetry property for f, g ∈ L2(C)
On the other hand, if χ is the characteristic function of the disk D(z,ε) with centre z and radius ε, then
Hence
By the Lebesgue differentiation theorem, the right hand side converges to Tf at the Lebesgue points of Tf.
Riesz transforms in higher dimensions
For f in the Schwartz space of Rn, the jth Riesz transform is defined by
where
Under the Fourier transform:
Thus Rj corresponds to the operator ∂jΔ−1/2, where Δ = −∂12 − ... −∂n2 denotes the Laplacian on Rn. By definition Rj is a bounded and skew-adjoint operator for the L2 norm and
The corresponding truncated operators
are uniformly bounded in the operator norm. This can either be proved directly or can be established by the Calderón−Zygmund method of rotations for the group SO(n).[24] This expresses the operators Rj and their truncations in terms of the Hilbert transforms in one dimension and its truncations. In fact if G = SO(n) with normalised Haar measure and H(1) is the Hilbert transform in the first coordinate, then
where φ(g) is the (1,j) matrix coefficient of g.
In particular for f ∈ L2, Rj,εf → Rjf in L2. Moreover, Rj,εf tends to Rj almost everywhere. This can be proved exactly as for the Hilbert transform by using the Poisson operators defined on L2(Rn) when Rn is regarded as the boundary of a halfspace in Rn+1. Alternatively it can be proved directly from the result for the Hilbert transform on R using the expression of Rj as an integral over G.[25][26]
The Poisson operators Ty on Rn are defined for y > 0 by[27]
They are given by convolution with the functions
Py is the Fourier transform of the function e−y|x|, so under the Fourier transform they correspond to multiplication by these functions and form a contraction semigroup on L2(Rn). Since Py is positive and integrable with integral 1, the operators Ty also define a contraction semigroup on each Lp space with 1 < p < ∞.
The Riesz transforms of the Poisson kernel can be computed
The operator RjTε is given by convolution with this function. It can be checked directly that the operators RjTε − Rj,ε are given by convolution with functions uniformly bounded in L1 norm. The operator norm of the difference is therefore uniformly bounded. We have (RjTε − Rj,ε)f → 0 at each Lebesgue point of f; while (Rj − RjTε)f → 0 at each Lebesgue point of Rjf. So Rj,εf → Rjf on the common Lebesgue points of f and Rjf.
Lp theory
Elementary proofs of M. Riesz theorem
The theorem of Marcel Riesz asserts that singular integral operators that are continuous for the L2 norm are also continuous in the Lp norm for 1 < p < ∞ and that the operator norms vary continuously with p.
Bochner's proof for Hilbert transform on the circle [28]
Once it is established that the operator norms of the Hilbert transform on Lp(T) are bounded for even integers, it follows from the Riesz–Thorin interpolation theorem and duality that they are bounded for all p with 1 < p < ∞ and that the norms vary continuously with p. Moreover, the arguments with the Poisson integral can be applied to show that the truncated Hilbert transforms Hε are uniformly bounded in operator norm and converge in the strong operator topology to H.
It is enough to prove the bound for real trigonometric polynomials without constant term:
Since f + iHf is a polynomial in eiθ without constant term
Hence, taking the real part and using Hölder's inequality:
So the M. Riesz theorem follows by induction for p an even integer and hence for all p with 1 < p < ∞.
Cotlar's proof for Hilbert transform on the line [29]
Once it is established that the operator norms of the Hilbert transform on Lp(R) are bounded when p is a power of 2, it follows from the Riesz–Thorin interpolation theorem and duality that they are bounded for all p with 1 < p < ∞ and that the norms vary continuously with p. Moreover, the arguments with the Poisson integral can be applied to show that the truncated Hilbert transforms Hε are uniformly bounded in operator norm and converge in the strong operator topology to H.
It is enough to prove the bound when f is a Schwartz function. In that case the following identity of Cotlar holds:
In fact, write f = f+ + f− according to the ±i eigenspaces of H. Since f ± iHf extend to holomorphic functions in the upper and lower half plane, so too do their squares. Hence
(Cotlar's identity can also be verified directly by taking Fourier transforms.)
Hence, assuming the M. Riesz theorem for p = 2n,
Since
for R sufficiently large, the M. Riesz theorem must also hold for p = 2n+1.
Exactly the same method works for the Hilbert transform on the circle.[30] The same identity of Cotlar is easily verified on trigonometric polynomials f by writing them as the sum of the terms with non-negative and negative exponents, i.e. the ±i eigenfunctions of H. The Lp bounds can therefore be established when p is a power of 2 and follow in general by interpolation and duality.
Calderón–Zygmund method of rotation
The method of rotation for Riesz transforms and their truncations applies equally well on Lp spaces for 1 < p < ∞. Thus these operators can be expressed in terms of the Hilbert transform on R and its truncations. The integration of the functions Φ from the group T or SO(n) into the space of operators on Lp is taken in the weak sense:
where f lies in Lp and g lies in the dual space Lq with 1/p + 1/q. It follows that Riesz transforms are bounded on Lp and that the differences with their truncations are also uniformly bounded. The continuity of the Lp norms of a fixed Riesz transform is a consequence of the Riesz–Thorin interpolation theorem.
Pointwise convergence
The proofs of pointwise convergence for Hilbert and Riesz transforms rely on the Lebesgue differentiation theorem, which can be proved using the Hardy-Littlewood maximal function.[31] The techniques for the simplest and best known case, namely the Hilbert transform on the circle, are a prototype for all the other transforms. This case is explained in detail here.
Let f be in Lp(T) for p > 1. The Lebesgue differentiation theorem states that
for almost all x in T.[32][33][34] The points at which this holds are called the Lebesgue points of f. Using this theorem it follows that if f is an integrable function on the circle, the Poisson integral Trf tends pointwise to f at each Lebesgue point of f. In fact, for x fixed, A(ε) is a continuous function on [0,π]. Continuity at 0 follows because x is a Lebesgue point and elsewhere because, if h is an integrable function, the integral of |h| on intervals of decreasing length tends to 0 by Hölder's inequality.
Letting r = 1 − ε, the difference can be estimated by two integrals:
The Poisson kernel has two important properties for ε small
The first integral is bounded by A(ε) by the first inequality so tends to zero as ε goes to 0; the second integral tends to 0 by the second inequality.
The same reasoning can be used to show that T1 − εHf – Hεf tends to zero at each Lebesgue point of f.[35] In fact the operator T1 − εHf has kernel Qr + i, where the conjugate Poisson kernel Qr is defined by
Hence
The conjugate Poisson kernel has two important properties for ε small
Exactly the same reasoning as before shows that the two integrals tend to 0 as ε → 0.
Combining these two limit formulas it follows that Hεf tends pointwise to Hf on the common Lebesgue points of f and Hf and therefore almost everywhere.[36][37][38]
Maximal functions
Much of the Lp theory has been developed using maximal functions and maximal transforms. This approach has the advantage that it also extends to L1 spaces in an appropriate "weak" sense and gives refined estimates in Lp spaces for p > 1. These finer estimates form an important part of the techniques involved in Lennart Carleson's solution in 1966 of Lusin's conjecture that the Fourier series of L2 functions converge almost everywhere.[39] In the more rudimentary forms of this approach, the L2 theory is given less precedence: instead there is more emphasis on the L1 theory, in particular its measure-theoretic and probabilistic aspects; results for other Lp spaces are deduced by a form of interpolation between L1 and L∞ spaces. The approach is described in numerous textbooks, including the classics Zygmund (1977) and Katznelson (2004). Katznelson's account is followed here for the particular case of the Hilbert transform of functions in L1(T), the case not covered by the development above.[40]
If f is an L1 function on the circle its maximal function is defined by[41]
f* is finite almost everywhere and is of weak L1 type. In fact for λ > 0 if
then[42]
where m denotes Lebesgue measure.
The Hardy−Littlewood inequality above leads to a proof that almost every point x of T is a Lebesgue point of an integrable function f, so that
In fact let
If g is continuous, then the ω(g) =0, so that ω(f − g) = ω(f). On the other hand, f can be approximated arbitrarily closely in L1 by continuous g. Then, using Chebychev's inequality,
The right hand side can be made arbitrarily small, so that ω(f) = 0 almost everywhere.
The Poisson integrals of an L1 function f satisfy[43]
It follows that Tr f tends to f pointwise almost everywhere. In fact let
If g is continuous, then the difference tends to zero everywhere, so Ω(f − g) = Ω(f). On the other hand, f can be approximated arbitrarily closely in L1 by continuous g. Then, using Chebychev's inequality,
The right hand side can be made arbitrarily small, so that Ω(f) = 0 almost everywhere. A more refined argument shows that convergence occurs at each Lebesgue point of f.
If f is integrable the conjugate Poisson integrals are defined and given by convolution by the kernel Qr. This defines Hf inside |z| < 1. To show that Hf has a radial limit for almost all angles,[44] consider
where f(z) denotes the extension of f by Poisson integral. F is holomorphic in the unit disk with |F(z)| ≤ 1. The restriction of F to a countable family of concentric circles gives a sequence of functions in L∞(T) which has a weak g limit in L∞(T) with Poisson integral F. By the L2 results, g is the radial limit for almost all angles of F. It follows that Hf(z) has a radial limit almost everywhere. This is taken as the definition of Hf on T, so that TrH f tends pointwise to H almost everywhere. The function Hf is of weak L1 type.[45]
The inequality used above to prove pointwise convergence for Lp function with 1 < p < ∞ make sense for L1 functions by invoking the maximal function. The inequality becomes
Let
If g is smooth, then the difference tends to zero everywhere, so ω(f − g) = ω(f). On the other hand, f can be approximated arbitrarily closely in L1 by smooth g. Then
The right hand side can be made arbitrarily small, so that ω(f) = 0 almost everywhere. Thus the difference for f tends to zero almost everywhere. A more refined argument can be given[46] to show that, as in case of Lp, the difference tends to zero at all Lebesgue points of f. In combination with the result for the conjugate Poisson integral, it follows that, if f is in L1(T), then Hεf converges to Hf almost everywhere, a theorem originally proved by Privalov in 1919.
General theory
Calderón & Zygmund (1952) introduced general techniques for studying singular integral operators of convolution type. In Fourier transform the operators are given by multiplication operators. These will yield bounded operators on L2 if the corresponding multiplier function is bounded. To prove boundedness on Lp spaces, Calderón and Zygmund introduced a method of decomposing L1 functions, generalising the rising sun lemma of F. Riesz. This method showed that the operator defined a continuous operator from L1 to the space of functions of weak L1. The Marcinkiewicz interpolation theorem and duality then implies that the singular integral operator is bounded on all Lp for 1 < p < ∞. A simple version of this theory is described below for operators on R. As de Leeuw (1965) showed, results on R can be deduced from corresponding results for T by restricting the multiplier to the integers, or equivalently periodizing the kernel of the operator. Corresponding results for the circle were originally established by Marcinkiewicz in 1939. These results generalize to Rn and Tn. They provide an alternative method for showing that the Riesz transforms, the higher Riesz transforms and in particular the Beurling transform define bounded operators on Lp spaces.[47]
Calderón-Zygmund decomposition
Let f be a non-negative integrable or continuous function on [a,b]. Let I = (a,b). For any open subinterval J of [a,b], let fJ denote the average of |f| over J. Let α be a positive constant greater than fI. Divide I into two equal intervals (omitting the midpoint). One of these intervals must satisfy fJ < α since their sum is 2fI so less than 2α. Otherwise the interval will satisfy α ≤ fJ < 2α. Discard such intervals and repeat the halving process with the remaining interval, discarding intervals using the same criterion. This can be continued indefinitely. The discarded intervals are disjoint and their union is an open set Ω. For points x in the complement, they lie in a nested set of intervals with lengths decreasing to 0 and on each of which the average of f is bounded by α. If f is continuous these averages tend to |f(x)|. If f is only integrable this is only true almost everywhere, for it is true at the Lebesgue points of f by the Lebesgue differentiation theorem. Thus f satisfies |f(x)| ≤ α almost everywhere on Ωc, the complement of Ω. Let Jn be the set of discarded intervals and define the "good" function g by
By construction |g(x)| ≤ 2α almost everywhere and
Combining these two inequalities gives
Define the "bad" function b by b = f − g. Thus b is 0 off Ω and equal to f minus its average on Jn. So the average of b on Jn is zero and
Moreover, since |b| ≥ α on Ω
The decomposition
is called the Calderón–Zygmund decomposition.[48]
Multiplier theorem
Let K(x) be a kernel defined on R\{0} such that
exists as a tempered distribution for f a Schwartz function. Suppose that the Fourier transform of T is bounded, so that convolution by W defines a bounded operator T on L2(R). Then if K satisfies Hörmander's condition
then T defines a bounded operator on Lp for 1 < p < ∞ and a continuous operator from L1 into functions of weak type L1.[49]
In fact by the Marcinkiewicz interpolation argument and duality, it suffices to check that if f is smooth of compact support then
Take a Calderón−Zygmund decomposition of f as above
with intervals Jn and with α = λμ, where μ > 0. Then
The term for g can be estimated using Chebychev's inequality:
If J* is defined to be the interval with the same centre as J but twice the length, the term for b can be broken up into two parts:
The second term is easy to estimate:
To estimate the first term note that
Thus by Chebychev's inequality:
By construction the integral of bn over Jn is zero. Thus, if yn is the midpoint of Jn, then by Hörmander's condition:
Hence
Combining the three estimates gives
The constant is minimized by taking
The Markinciewicz interpolation argument extends the bounds to any Lp with 1 < p < 2 as follows.[50] Given a > 0, write
where fa = f if |f| < a and 0 otherwise and fa = f if |f| ≥ a and 0 otherwise. Then by Chebychev's inequality and the weak type L1 inequality above
Hence
By duality
Continuity of the norms can be shown by a more refined argument[51] or follows from the Riesz–Thorin interpolation theorem.
Notes
- ↑ Torchinsky 2004, pp. 65–66
- ↑ Bell 1992, pp. 14–15
- ↑ Krantz 1999
- ↑ Torchinsky 1986
- ↑ Stein & Rami 2005, pp. 112–114
- ↑ See:
- ↑ Garnett 2007, p. 102
- ↑ See:
- ↑ Stein & Shakarchi 2005, pp. 213–221
- ↑ Hörmander 1990
- ↑ Titchmarsh & 1939 102–105
- ↑ See:
- Krantz 1999
- Torchinsky 1986
- Duoandikoetxea 2001, pp. 49–51
- ↑ Stein & Shakarchi 2005, pp. 112–114
- ↑ Stein & Weiss 1971
- ↑ Astala, Ivaniecz & Martin 2009, pp. 101–102
- ↑ Grafakos 2005
- ↑ Stein & Weiss 1971
- ↑ Stein & Weiss 1971, p. 51
- ↑ Grafakos 2008
- ↑ Stein & Weiss 1971, pp. 222–223
- ↑ Stein & Weiss 1971
- ↑ Astala, Iwaniecz & Martin 2009, pp. 93–95
- ↑ Astala, Iwaniecz & Martin 2009, pp. 97–98
- ↑ Grafokos 2008, pp. 272–274
- ↑ Grafakos 2008
- ↑ Stein & Weiss 1971, pp. 222–223, 236–237
- ↑ Stein & Weiss 1971
- ↑ Grafakos 2005, p. 215−216
- ↑ Grafakos 2005, p. 255−257
- ↑ Gohberg & Krupnik 1992, pp. 19–20
- ↑ See:
- Stein & Weiss 1971, pp. 12–13
- Torchinsky 2004
- ↑ Torchinsky 2005, pp. 41–42
- ↑ Katznelson 2004, pp. 10–21
- ↑ Stein & Shakarchi 112-114
- ↑ Garnett 2007, pp. 102–103
- ↑ Krantz 1999
- ↑ Torchinsky 1986
- ↑ Stein & Shakarchi 2005, pp. 112–114
- ↑ Arias de Reyna 2002
- ↑ See also:
- ↑ Krantz 1999, p. 71
- ↑ Katznelson 2004, pp. 74–75
- ↑ Katznelson 2004, p. 76
- ↑ Katznelson 2004, p. 64
- ↑ Katznelson 2004, p. 66
- ↑ Katznelson 2004, pp. 78–79
- ↑ See:
- ↑ Torchinsky 2005, pp. 74–76,84–85
- ↑ Grafakos 2008, pp. 290–293
- ↑ Hörmander 1990, p. 245
- ↑ Torchinsky 2005, pp. 87–91
References
- Ahlfors, Lars V. (1966), Lectures on quasiconformal mappings, Van Nostrand Mathematical Studies 10, Van Nostrand
- Arias de Reyna, Juan (2002), Pointwise Convergence of Fourier Series, Lecture Notes in Mathematics 1785, Springer, ISBN 3540432701
- Astala, Kari; Iwaniec, Tadeusz; Martin, Gaven (2009), Elliptic partial differential equations and quasiconformal mappings in the plane, Princeton Mathematical Series 48, Princeton University Press, ISBN 978-0-691-13777-3
- Bell, Steven R. (1992), The Cauchy transform, potential theory, and conformal mapping, Studies in Advanced Mathematics, CRC Press, ISBN 0-8493-8270-X
- Calderón, Alberto; Zygmund, Antoni (1952), "On the existence of certain singular integrals", Acta Math. 88: 85–139, doi:10.1007/bf02392130
- Calderón, Alberto (1966), "Singular integrals", Bull. Amer. Math. Soc. 72: 427–465, doi:10.1090/s0002-9904-1966-11492-1
- de Leeuw, Karel (1965), "On Lp multipliers", Ann. of Math. 81: 364–379
- Devinatz, Allen (1967), On Wiener-Hopf operators, Functional Analysis (Proc. Conf., Irvine, Calif., 1966), Academic Press, pp. 81–118
- Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 0-8218-2172-5
- Garnett, John B. (2007), Bounded analytic functions, Graduate Texts in Mathematics 236, Springer, ISBN 978-0-387-33621-3
- Gohberg, Israel; Krupnik, Naum (1968), "Norm of the Hilbert transformation in the Lp space", Funct. Anal. Appl. 2: 180–181
- Gohberg, Israel; Krupnik, Naum (1992), One-dimensional linear singular integral equations, I. Introduction, Operator Theory: Advances and Applications 53, Birkhäuser, ISBN 3-7643-2584-4
- Grafakos, Loukas (2008), Classical Fourier Analysis (2nd ed.), Springer, ISBN 978-0-387-09431-1
- Hörmander, Lars (1960), "Estimates for translation invariant operators in Lp spaces", Acta Mathematica 104: 93–140, doi:10.1007/bf02547187
- Hörmander, Lars (1990), The analysis of linear partial differential operators, I. Distribution theory and Fourier analysis (2nd ed.), Springer-Verlag, ISBN 3-540-52343-X
- Iwaniec, Tadeusz; Martin, Gaven (1996), "Riesz transforms and related singular integrals", J. reine angew. Math. 473: 25–57
- Katznelson, Yitzhak (2004), An Introduction to Harmonic Analysis, Cambridge University Press, ISBN 978-0-521-54359-0
- Krantz, Steven G. (1999), A panorama of harmonic analysis, Carus Mathematical Monographs 27, Mathematical Association of America, ISBN 0-88385-031-1
- Mateu, Joan; Verdera, Joan (2006), "Lp and weak L1 estimates for the maximal Riesz transform and the maximal Beurling transform", Math. Res. Lett. 13: 957–966, doi:10.4310/mrl.2006.v13.n6.a10
- Mikhlin, Solomon G. (1965), Multidimensional singular integrals and integral equations, International Series of Monographs in Pure and Applied Mathematics 83, Pergamon Press
- Mikhlin, Solomon G.; Prössdorf, Siegfried (1986), Singular integral operators, Springer-Verlag, ISBN 3-540-15967-3
- Nikolski, N. K. (1986), Treatise on the shift operator. Spectral function theory, Grundlehren der Mathematischen Wissenschaften 273, Springer-Verlag, ISBN 3-540-15021-8
- Pressley, Andrew; Segal, Graeme (1986), Loop groups, Oxford University Press, ISBN 0-19-853535-X
- Rosenblum, Marvin; Rovnyak, James (1997), Hardy classes and operator theory, Dover, ISBN 0-486-69536-0
- Rosenblum, Marvin; Rovnyak, James (1994), Topics in Hardy classes and univalent functions, Birkhäuser, ISBN 3-7643-5111-X
- Segal, Graeme (1981), "Unitary representations of some infinite-dimensional groups", Comm. Math. Phys. 80: 301–342, doi:10.1007/bf01208274
- Stein, Elias M. (1970), Singular Integrals and Differentiability Properties of Functions, Princeton University Press
- Stein, Elías M.; Weiss, Guido L. (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, ISBN 069108078X
- Stein, Elias M.; Shakarchi, Rami (2005), Real Analysis: Measure Theory, Integration, and Hilbert Spaces, Princeton Lectures in Analysis 3, Princeton University Press, ISBN 0691113866
- Titchmarsh, E. C. (1939), The Theory of Functions (2nd ed.), Oxford University Press, ISBN 0198533497
- Torchinsky, Alberto (2004), Real-Variable Methods in Harmonic Analysis, Dover, ISBN 0-486-43508-3
- Vekua, I. N. (1962), Generalized analytic functions, Pergamon Press
- Zygmund, Antoni (1977), Trigonometric series. Vol. I, II (2nd ed.), Cambridge University Press, ISBN 0-521-07477-0
- Zygmund, Antoni (1971), Intégrales singulières, Lecture Notes in Mathematics 204, Springer-Verlag
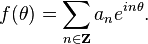
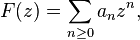
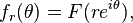
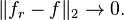
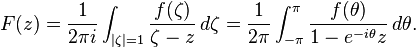
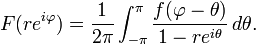
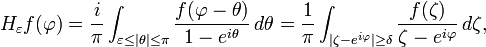
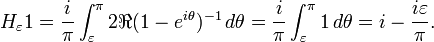
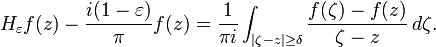
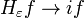
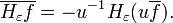
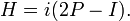
![\displaystyle{(1-e^{i\theta})^{-1}= [(1-e^{i\theta})^{-1} -i\theta^{-1}] +i\theta^{-1}.}](../I/m/6113d47a15dbb110696e8d54cd78575d.png)
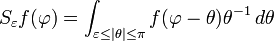
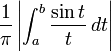
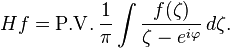
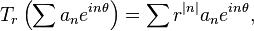
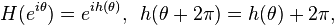
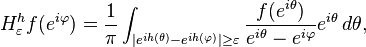
![(VH^h_\varepsilon V^{-1}- H_\varepsilon) f(e^{i\varphi}) = {1\over \pi}\int_{|e^{i\theta}-e^{i\varphi}| \ge \varepsilon}\left[{g^\prime(\theta) e^{ig(\theta)} \over e^{ig(\theta)} - e^{ig(\varphi)}} - {e^{i\theta} \over e^{i\theta} - e^{i\varphi} }\right]\,f(e^{i\theta})\, d\theta.](../I/m/8186b2c47f7d57ce36fdb7ebcb2d6e4e.png)
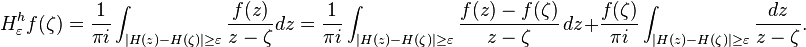
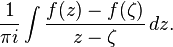
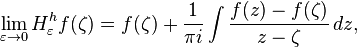
![(VH V^{-1}- H) f(e^{i\varphi}) = \frac{1}{\pi} \int \left[{g^\prime(\theta) e^{ig(\theta)} \over e^{ig(\theta)} - e^{ig(\varphi)}} - {e^{i\theta} \over e^{i\theta} - e^{i\varphi}}\right]\,f(e^{i\theta})\, d\theta.](../I/m/1ea0f096341d9f510002f082e879c64f.png)
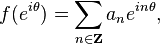
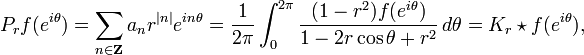
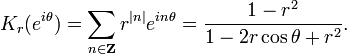
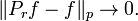
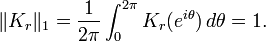
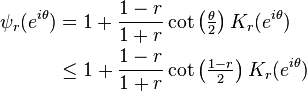
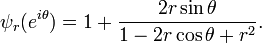
![\widehat{H_{\mathbf{R}} f} = \left (i\chi_{[0,\infty)} -i\chi_{(-\infty,0]} \right ) \widehat{f},](../I/m/fc4a2205bbca3089c77c4b649fbdffbb.png)
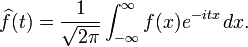
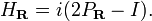
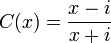
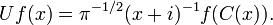
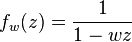
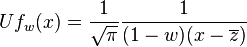
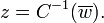
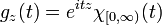
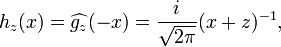
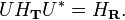
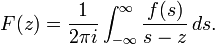
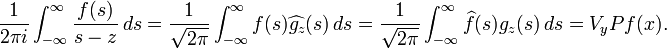
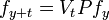
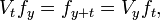
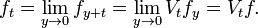
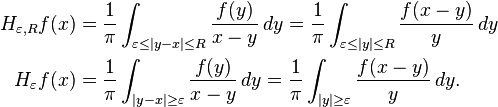
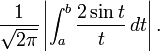
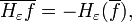
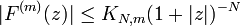
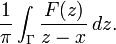

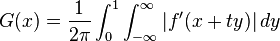

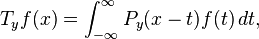
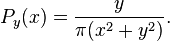
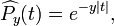
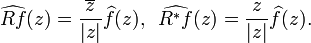
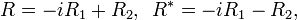
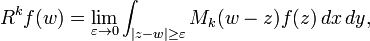
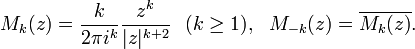
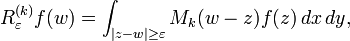
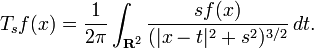
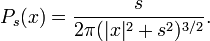
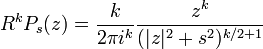
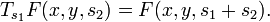
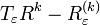
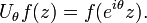
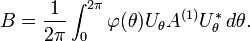
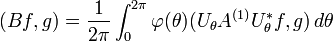
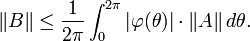
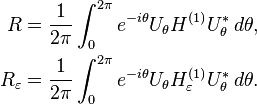

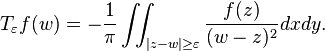
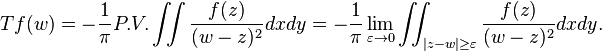
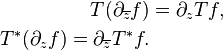
![\begin{align}
T_\varepsilon(\Omega)f(w) &= -\frac{1}{\pi} \iint_{D\backslash V_\varepsilon} \left [{\varphi^\prime(w)\varphi^\prime(z) \over (\varphi(z)-\varphi(w))^2}f(z)\right ]dxdy,\\
T_\varepsilon(D)f(w) &=-{1\over \pi} \iint_{D\backslash U_\varepsilon} {f(z) \over (z-w)^2}dxdy,
\end{align}](../I/m/010b103044b7c4cc38210e30ec6c5ca8.png)
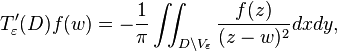
![K(w,z)=-{1\over \pi} \left[{\varphi^\prime(w)\varphi^\prime(z)\over (\varphi(z)-\varphi(w))^2} -{1\over (z-w)^2}\right].](../I/m/5d5dc252571b1e4a46afc1873f699bc6.png)
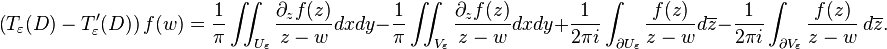
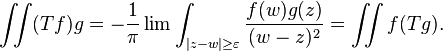
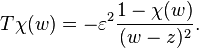
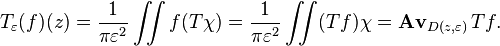
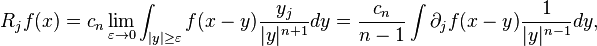
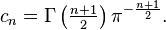
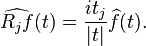
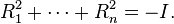
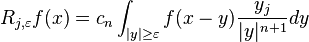
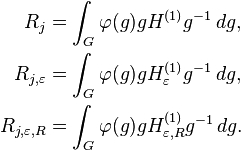
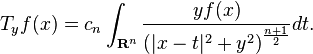
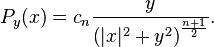
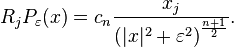
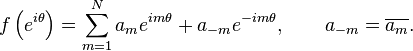
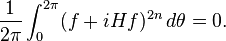
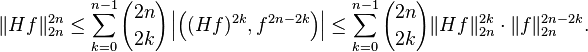
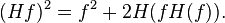
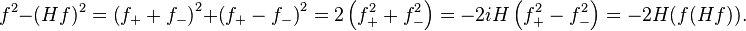
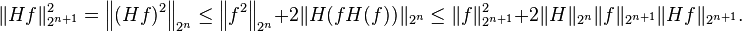

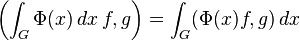
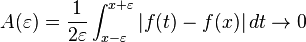
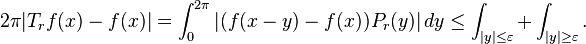
![\begin{align}
\sup_{y\in [-\varepsilon,\varepsilon]} |P_{1-\varepsilon}(y)| &\le \varepsilon^{-1}. \\
\sup_{y\notin (-\varepsilon,\varepsilon)} |P_{1-\varepsilon}(y)| &\to 0.
\end{align}](../I/m/005aa62b104d6c799bde251b5ff1103d.png)
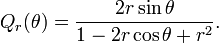
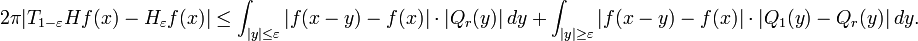
![\begin{align}
\sup_{y\in [-\varepsilon,\varepsilon]} |Q_{1-\varepsilon}(y)| &\le \varepsilon^{-1}.\\
\sup_{y\notin (-\varepsilon,\varepsilon)} |Q_1(y)-Q_{1-\varepsilon}(y)| &\to 0.
\end{align}](../I/m/5d5b06eca4dce7f9c42ad40d86824b60.png)