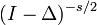Bessel potential

In mathematics, the Bessel potential is a potential (named after Friedrich Wilhelm Bessel) similar to the Riesz potential but with better decay properties at infinity.

If s is a complex number with positive real part then the Bessel potential of order s is the operator

where Δ is the Laplace operator and the fractional power is defined using Fourier transforms.

Yukawa potentials are particular cases of Bessel potentials for 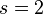in the 3-dimensional space.

See also

• Riesz potential
• Fractional integration
• Sobolev space
• Fractional Schrödinger equation

References

• Duduchava, R. (2001), "Bessel potential operator", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• Grafakos, Loukas (2009), Modern Fourier analysis, Graduate Texts in Mathematics 250 (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-0-387-09434-2, ISBN 978-0-387-09433-5, MR 2463316 
• Hedberg, L.I. (2001), "Bessel potential space", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• Solomentsev, E.D. (2001), "B/b015870", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• Stein, Elias (1970), Singular integrals and differentiability properties of functions, Princeton, NJ: Princeton University Press, ISBN 0-691-08079-8