Bernays–Schönfinkel class
The Bernays–Schönfinkel class (also known as Bernays–Schönfinkel-Ramsey class) of formulas, named after Paul Bernays and Moses Schönfinkel (and Frank P. Ramsey), is a decidable fragment of first-order logic formulas.
It is the set of satisfiable formulas which, when written in prenex normal form, have an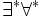 
quantifier prefix and do not contain any function symbols.
This class of logic formulas is also sometimes referred as effectively propositional (EPR) since it can be effectively translated into propositional logic formulas by a process of grounding or instantiation.
The decision problem for this class is NEXPTIME-complete.[1]
See also
References
- ↑ Harry R. Lewis, Complexity Results for Classes of Quantificational Formulas, J. Computer and System Sciences, 21, 317-353 (1980) doi:10.1016/0022-0000(80)90027-6
- Ramsey, F. (1930), "On a problem in formal logic", Proc. London Math. Soc. 30: 264–286, doi:10.1112/plms/s2-30.1.264
- Piskac, R.; de Moura, L.; Bjorner, N. (December 2008), "Deciding Effectively Propositional Logic with Equality" (PDF), Microsoft Research Technical Report (2008-181)
This article is issued from Wikipedia - version of the Wednesday, February 05, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.