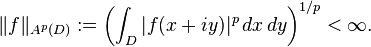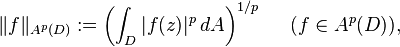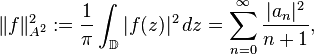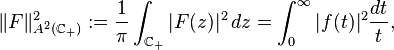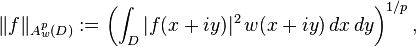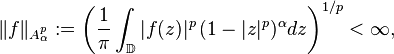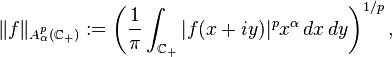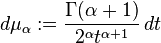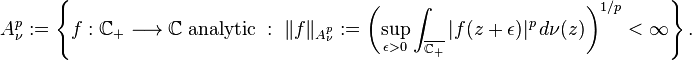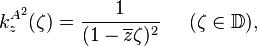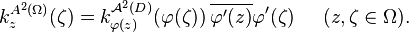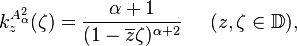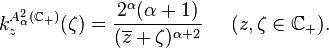Bergman space

In complex analysis, functional analysis and operator theory, a Bergman space is a function space of holomorphic functions in a domain D of the complex plane that are sufficiently well-behaved at the boundary that they are absolutely integrable. Specifically, for $0 < p < \infty$ , the Bergman space $A p (D)$ is the space of all holomorphic functions $f$ in D for which the p-norm is finite:

\|f\|_{A^p(D)} := \left(\int_D |f(x+iy)|^p\,dx\,dy\right)^{1/p} < \infty.

The quantity 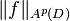$\|f\|_{A^p(D)}$ is called the norm of the function $f$ ; it is a true norm if $p \geq 1$ . Thus $A p (D)$ is the subspace of holomorphic functions that are in the space L^p(D). The Bergman spaces are Banach spaces, which is a consequence of the estimate, valid on compact subsets K of D:

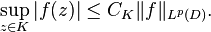
$\sup_{z\in K} |f(z)| \le C_K\|f\|_{L^p(D)}.$

(1)

Thus convergence of a sequence of holomorphic functions in $L p (D)$ implies also compact convergence, and so the limit function is also holomorphic.

If $p = 2$ , then $A p (D)$ is a reproducing kernel Hilbert space, whose kernel is given by the Bergman kernel.

Special cases and generalisations

If the domain $D$ is bounded, then the norm is often given by

\|f\|_{A^p(D)} := \left(\int_D |f(z)|^p\,dA\right)^{1/p} \; \; \; \; \; (f \in A^p(D)),

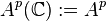where $A$ is a normalised Lebesgue measure of the complex plane, i.e. $dA = dz /Area(D)$ </. Alternatively $dA = dz / π$ is used, regardless of the area of $D$ . The Bergman space is usually defined on the open unit disk $\mathbb{D}$ of the complex plane, in which case $A^p(\mathbb{C}):=A^p$ . In the Hilbert space case, given 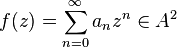$f(z)= \sum_{n=0}^\infty a_n z^n \in A^2$ , we have

\|f\|^2_{A^2} := \frac{1}{\pi} \int_\mathbb{D} |f(z)|^2 \, dz = \sum_{n=0}^\infty \frac{|a_n|^2}{n+1},

that is, $A 2$ is isometrically isomorphic to the weighted ℓ^p(1/(n+1)) space.^[1] In particular the polynomials are dense in $A 2$ . Similarly, if $D = ℂ +)$ , the right (or the upper) complex half-plane, then

\|F\|^2_{A^2(\mathbb{C}_+)} := \frac{1}{\pi} \int_{\mathbb{C}_+} |F(z)|^2 \, dz = \int_0^\infty |f(t)|^2\frac{dt}{t},

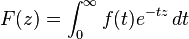where $F(z)= \int_0^\infty f(t)e^{-tz} \, dt$ , that is, $A 2 (ℂ +)$ is isometrically isomorphic to the weighted L^p_1/t (0,∞) space (via the Laplace transform).^[2]^[3]

The weighted Bergman space $A p (D)$ is defined in an analogous way,^[1] i.e.

\|f\|_{A^p_w (D)} := \left( \int_D |f(x+iy)|^2 \, w(x+iy) \, dx \, dy \right)^{1/p},

provided that $w : D \to [0, \infty)$ is chosen in such way, that 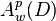$A^p_w(D)$ is a Banach space (or a Hilbert space, if $p = 2$ ). In case where 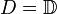$D= \mathbb{D}$ , by a weighted Bergman space 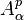$A^p_\alpha$ ^[4] we mean the space of all analytic functions $f$ such that

\|f\|_{A^p_\alpha} := \left( \frac{1}{\pi}\int_\mathbb{D} |f(z)|^p \, (1-|z|^p)^\alpha dz \right)^{1/p} < \infty,

and similarly on the right half-plane (i.e. 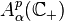$A^p_\alpha(\mathbb{C}_+)$ ) we have^[5]

\|f\|_{A^p_\alpha(\mathbb{C}_+)} := \left( \frac{1}{\pi}\int_{\mathbb{C}_+} |f(x+iy)|^p x^\alpha \, dx \, dy \right)^{1/p},

and this space is isometrically isomorphic, via the Laplace transform, to the space 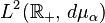$L^2(\mathbb{R}_+, \, d\mu_\alpha)$ ,^[6]^[7] where

d\mu_\alpha := \frac{\Gamma(\alpha+1)}{2^\alpha t^{\alpha+1}} \, dt

(here $Γ$ denotes the Gamma function).

Further generalisations are sometimes considered, for example 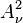$A^2_\nu$ denotes a weighted Bergman space (often called a Zen space^[3]) with respect to a translation-invariant positive regular Borel measure 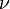$\nu$ on the closed right complex half-plane 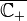$\overline{\mathbb{C}_+}$ , that is

A^p_\nu := \left\{ f : \mathbb{C}_+ \longrightarrow \mathbb{C} \; \text{analytic} \; : \; \|f\|_{A^p_\nu} := \left( \sup_{\epsilon>0} \int_{\overline{\mathbb{C}_+}} |f(z+\epsilon)|^p \, d\nu(z) \right)^{1/p} < \infty \right\}.

Reproducing kernels

The reproducing kernel 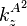$k_z^{A^2}$ of $A 2$ at point 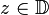$z \in \mathbb{D}$ is given by^[1]

k_z^{A^2}(\zeta)=\frac{1}{(1-\overline{z}\zeta)^2} \; \; \; \; \; (\zeta \in \mathbb{D}),

and similarly for 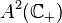$A^2(\mathbb{C}_+)$ we have^[5]

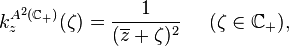k_z^{A^2(\mathbb{C}_+)}(\zeta)=\frac{1}{(\overline{z}+\zeta)^2} \; \; \; \; \; (\zeta \in \mathbb{C}_+),

In general, if $\varphi$ maps a domain $\Omega$ conformally onto a domain $D$ , then^[1]

k^{A^2(\Omega)}_z (\zeta) = k^{\mathcal{A}^2(D)}_{\varphi(z)}(\varphi(\zeta)) \, \overline{\varphi'(z)}\varphi'(\zeta) \; \; \; \; \; (z, \zeta \in \Omega).

In weighted case we have^[4]

k_z^{A^2_\alpha} (\zeta) = \frac{\alpha+1}{(1-\overline{z}\zeta)^{\alpha+2}} \; \; \; \; \; (z, \zeta \in \mathbb{D}),

and^[5]

k_z^{A^2_\alpha(\mathbb{C}_+)} (\zeta) = \frac{2^\alpha(\alpha+1)}{(\overline{z}+\zeta)^{\alpha+2}} \; \; \; \; \; (z, \zeta \in \mathbb{C}_+).

References

1 2 3 4 Duren, Peter L.; Schuster, Alexander (2004), Bergman spaces, Mathematical Series and Monographs, American Mathematical Society, ISBN 978-0-8218-0810-8
↑ Duren, Peter L. (1969), Extension of a theorem of Carleson (PDF) 75, Bulletin of the American Mathematical Society, pp. 143–146
1 2 Jacob, Brigit; Partington, Jonathan R.; Pott, Sandra (2013-02-01), On Laplace-Carleson embedding theorems 264 (3), Journal of Functional Analysis, pp. 783–814
1 2 Cowen, Carl; MacCluer, Barbara (1995-04-27), Composition Operators on Spaces of Analytic Functions, Studies in Advanced Mathematics, CRC Press, p. 27, ISBN 9780849384929
1 2 3 Elliott, Sam J.; Wynn, Andrew (2011), Composition Operators on the Weighted Bergman Spaces of the Half-Plane 54 (2), Proceedings of the Edinburgh Mathematical Society, pp. 374–379
↑ Duren, Peter L.; Gallardo-Gutiérez, Eva A.; Montes-Rodríguez, Alfonso (2007-06-03), A Paley-Wiener theorem for Bergman spaces with application to invariant subspaces (PDF) 39 (3), Bulletin of the London Mathematical Society, pp. 459–466
↑ Gallrado-Gutiérez, Eva A.; Partington, Jonathan R.; Segura, Dolores (2009), Cyclic vectors and invariant subspaces for Bergman and Dirichlet shifts (PDF) 62 (1), Journal of Operator Theory, pp. 199–214

Bergman space

Special cases and generalisations

Reproducing kernels

References

Further reading

See also