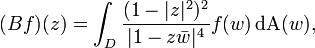Berezin transform

In mathematics — specifically, in complex analysis — the Berezin transform is an integral operator acting on functions defined on the open unit disk D of the complex plane C. Formally, for a function f : D → C, the Berezin transform of f is a new function Bf : D → C defined at a point z ∈ D by

(B f)(z) = \int_{D} \frac{(1 - | z |^{2})^{2}}{| 1 - z \bar{w} |^{4}} f(w) \, \mathrm{dA} (w),

where w denotes the complex conjugate of w and $dA$ is the area measure. It is named after Felix Alexandrovich Berezin.

References

Hedenmalm, Haakan; Korenblum, Boris; Zhu, Kehe (2000). Theory of Bergman spaces. Graduate Texts in Mathematics 199. New York: Springer-Verlag. pp. 28–51. ISBN 0-387-98791-6. MR 1758653.

External links

Weisstein, Eric W., "Berezin transform", MathWorld.

This article is issued from Wikipedia - version of the Saturday, July 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.