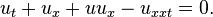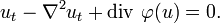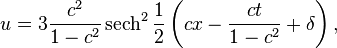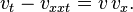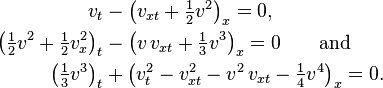Benjamin–Bona–Mahony equation

The upper graph is for a frame of reference moving with the average celerity of the solitary waves. The envelope of the overtaking waves is shown in grey: note that the maximum wave height reduces during the interaction.
The lower graph (with a different vertical scale and in a stationary frame of reference) shows the oscillatory tail produced by the interaction.[1] Thus, the solitary wave solutions of the BBM equation are not solitons.

The Benjamin–Bona–Mahony equation (or BBM equation) – also known as the regularized long-wave equation (RLWE) – is the partial differential equation
This equation was studied in Benjamin, Bona, and Mahony (1972) as an improvement of the Korteweg–de Vries equation (KdV equation) for modeling long surface gravity waves of small amplitude – propagating uni-directionally in 1+1 dimensions. They show the stability and uniqueness of solutions to the BBM equation. This contrasts with the KdV equation, which is unstable in its high wavenumber components. Further, while the KdV equation has an infinite number of integrals of motion, the BBM equation only has three.[2][3]
Before, in 1966, this equation was introduced by Peregrine, in the study of undular bores.[4]
A generalized n-dimensional version is given by[5][6]
where  is a sufficiently smooth function from
is a sufficiently smooth function from 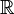 to
to  . Avrin & Goldstein (1985) proved global existence of a solution in all dimensions.
. Avrin & Goldstein (1985) proved global existence of a solution in all dimensions.
Solitary wave solution
The BBM equation possesses solitary wave solutions of the form:[3]
where sech is the hyperbolic secant function and 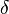 is a phase shift (by an initial horizontal displacement). For
is a phase shift (by an initial horizontal displacement). For 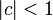 , the solitary waves have a positive crest elevation and travel in the positive
, the solitary waves have a positive crest elevation and travel in the positive  -direction with velocity
-direction with velocity 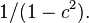 These solitary waves are not solitons, i.e. after interaction with other solitary waves, an oscillatory tail is generated and the solitary waves have changed.[1][3]
These solitary waves are not solitons, i.e. after interaction with other solitary waves, an oscillatory tail is generated and the solitary waves have changed.[1][3]
Hamiltonian structure
The BBM equation has a Hamiltonian structure, as it can be written as:[7]
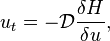 with Hamiltonian
with Hamiltonian 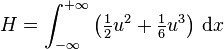 and operator
and operator 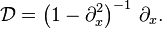
Here 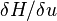 is the variation of the Hamiltonian
is the variation of the Hamiltonian  with respect to
with respect to 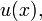 and
and 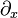 denotes the partial differential operator with respect to
denotes the partial differential operator with respect to 
Conservation laws
The BBM equation possesses exactly three independent and non-trivial conservation laws.[3] First 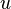 is replaced by
is replaced by 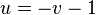 in the BBM equation, leading to the equivalent equation:
in the BBM equation, leading to the equivalent equation:
The three conservation laws then are:[3]
Which can easily expressed in terms of 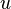 by using
by using 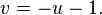
Notes
- 1 2 Bona, Pritchard & Scott (1980)
- ↑ Benjamin, Bona, and Mahony (1972)
- 1 2 3 4 5 Olver (1979)
- ↑ Peregrine (1966)
- ↑ Goldstein & Wichnoski (1980)
- ↑ Avrin & Goldstein (1985)
- ↑ Olver, P.J. (1980), "On the Hamiltonian structure of evolution equations", Mathematical Proceedings of the Cambridge Philosophical Society 88 (1): 71–88, Bibcode:1980MPCPS..88...71O, doi:10.1017/S0305004100057364
References
- Avrin, J.; Goldstein, J.A. (1985), "Global existence for the Benjamin–Bona–Mahony equation in arbitrary dimensions", Nonlinear Analysis 9 (8): 861–865, doi:10.1016/0362-546X(85)90023-9, MR 0799889
- Benjamin, T. B.; Bona, J. L.; Mahony, J. J. (1972), "Model Equations for Long Waves in Nonlinear Dispersive Systems", Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 272 (1220): 47–78, Bibcode:1972RSPTA.272...47B, doi:10.1098/rsta.1972.0032, ISSN 0962-8428, JSTOR 74079
- Bona, J. L.; Pritchard, W. G.; Scott, L. R. (1980), "Solitary‐wave interaction", Physics of Fluids 23 (3): 438–441, Bibcode:1980PhFl...23..438B, doi:10.1063/1.863011
- Goldstein, J.A.; Wichnoski, B.J. (1980), "On the Benjamin–Bona–Mahony equation in higher dimensions", Nonlinear Analysis 4 (4): 665–675, doi:10.1016/0362-546X(80)90067-X
- Olver, P. J. (1979), "Euler operators and conservation laws of the BBM equation", Mathematical Proceedings of the Cambridge Philosophical Society 85: 143–160, Bibcode:1979MPCPS..85..143O, doi:10.1017/S0305004100055572
- Peregrine, D.H. (1966), "Calculations of the development of an undular bore", Journal of Fluid Mechanics 25 (2): 321–330, Bibcode:1966JFM....25..321P, doi:10.1017/S0022112066001678
- Zwillinger, D. (1998), Handbook of differential equations (3rd ed.), Boston, MA: Academic Press, pp. 174 & 176, ISBN 978-0-12-784396-4, MR 0977062 (Warning: On p. 174 Zwillinger misstates the Benjamin–Bona–Mahony equation, confusing it with the similar KdV equation.)