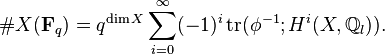Behrend's trace formula

In algebraic geometry, Behrend's formula is a generalization of the Grothendieck–Lefschetz trace formula to a smooth algebraic stack over a finite field, conjectured in 1993 ^[1] and proven in 2003 ^[2] by Kai Behrend. Unlike the classical one, the formula counts points in the "stacky way"; it takes into account the presence of nontrivial automorphisms.

The desire for the formula comes from the fact that it applies to the moduli stack of principal bundles on a curve over a finite field (in some instances indirectly, via the Harder–Narasimhan stratification, as the moduli stack is not of finite type.^[3]^[4]) See the moduli stack of principal bundles and references therein for the precise formulation in this case.

Deligne found an example^[5] that shows the formula may be interpreted as a sort of the Selberg trace formula.

A proof of the formula in the context of the six operations formalism developed by Laszlo and Olsson^[6] is given by Shenghao Sun.^[7]

Formulation

By definition, if C is a category in which each object has finitely many automorphisms, the number of points in 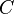$C$ is denoted by

\# C = \sum_p {1 \over \# \operatorname{Aut}(p)},

with the sum running over representatives p of all isomorphism classes in C. (The series may diverge in general.) The formula states: for a smooth algebraic stack X of finite type over a finite field 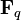$\mathbf{F}_q$ and the "arithmetic" Frobenius 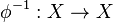$\phi^{-1}: X \to X$ , i.e., the inverse of the usual geometric Frobenius $\phi$ in Grothendieck's formula,^[8]^[9]

\# X (\mathbf{F}_q) = q^{\operatorname{dim}X} \sum_{i=0}^{\infty} (-1)^i \operatorname{tr}(\phi^{-1}; H^i(X, \mathbb{Q}_l)).

Here, it is crucial that the cohomology of a stack is with respect to the smooth topology (not etale).

When X is a variety, the smooth cohomology is the same as etale one and, via the Poincaré duality, this is equivalent to Grothendieck's trace formula. (But the proof relies on Grothendieck's formula, so this does not subsume Grothendieck's.)

Simple example

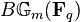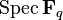Consider $B \mathbb{G}_m = [\operatorname{Spec} \mathbf{F}_q/\mathbb{G}_m]$ , the classifying stack of the multiplicative group scheme (that is, $\mathbb{G}_m(R) = R^\times$ ). By definition, $B \mathbb G_m(\mathbf{F}_q)$ is the category of principal $\mathbb{G}_m$ -bundles over $\operatorname{Spec} \mathbf{F}_q$ , which has only one isomorphism class (since all such bundles are trivial by Lang's theorem). 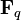Its group of automorphisms is $\mathbb{G}_m$ , which means that the number of $\mathbf{F}_q$ -isomorphisms is $\#\mathbb{G}_m(\mathbf{F}_q) = \#\mathbf{F}_q^\times = q-1$ .

On the other hand, we may compute the l-adic cohomology of 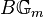$B\mathbb{G}_m$ directly. We remark that in the topological setting, we have 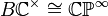$B\mathbb{C}^\times \cong \mathbb{CP}^\infty$ (where 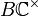$B\mathbb C^\times$ now denotes the usual classifying space of a topological group), whose rational cohomology ring is a polynomial ring in one generator (Borel's theorem), but we shall not use this directly. If we wish to stay in the world of algebraic geometry, we may instead "approximate" 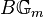$B\mathbb{G}_m$ by projective spaces of larger and larger dimension. 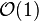Thus we consider the map $B\mathbb{G}_m \to \mathbb{P}^N$ induced by the $\mathbb{G}_m$ -bundle corresponding to $\mathcal O(1)$ . This map induces an isomorphism in cohomology in degrees up to 2N. Thus the even (resp. odd) Betti numbers of 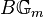$B \mathbb{G}_m$ are 1 (resp. 0), and the l-adic Galois representation on the (2n)th cohomology group is the nth power of the cyclotomic character. The second part is a consequence of the fact that the cohomology of $\mathbb P^N$ is generated by algebraic cycle classes. This shows that

\sum_{i \ge 0} (-1)^i \operatorname{tr}(\phi^{-1}; H^i(B\mathbb G_m, \mathbb{Q}_l)) = 1 + 1 / q + 1/q^2 + \cdots = {q \over {q-1}}.

Note that 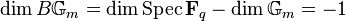$\dim B \mathbb{G}_m = \dim \operatorname{Spec} \mathbf{F}_q - \dim \mathbb{G}_m = -1$ . Multiplying by 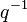$q^{-1}$ , one obtains the predicted equality.

Notes

↑ Behrend, K. The Lefschetz Trace Formula for the Moduli Stack of Principal Bundles. PhD dissertation.
↑ Behrend, K. Derived l-adic categories for algebraic stacks. Memoirs of the American Mathematical Society Vol. 163, 2003
↑ K. Behrend, A. Dhillon, Connected components of moduli stacks of torsors via Tamagawa numbers
↑ http://www.math.harvard.edu/~lurie/282ynotes/LectureIII-Cohomology.pdf
↑ Behrend 2003, Proposition 6.4.11
↑
- Laszlo, Yves; Olsson, Martin (2006). "The six operations for sheaves on Artin stacks I: Finite Coefficients". arXiv:math/0512097v2.
↑ Sun 2011
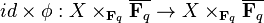↑ To define Frobenius $\phi$ on a stack X, let $\phi: \overline{\mathbf{F}_q} \to \overline{\mathbf{F}_q}, x \mapsto x^q$ . Then we have $id \times \phi: X \times_{\mathbf{F}_q} \overline{\mathbf{F}_q} \to X \times_{\mathbf{F}_q} \overline{\mathbf{F}_q}$ , which is the Frobenius on X, also denoted by $\phi$ .
↑ Behrend 2003, Corollary 6.4.10

References

Shenghao, Sun (2011). "L-series of Artin stacks over finite fields". arXiv:1008.3689v2.

This article is issued from Wikipedia - version of the Monday, January 25, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.