Behavior tree (artificial intelligence, robotics and control)
A behavior tree (BT) is a mathematical model of plan execution used in computer science, robotics, control systems and video games. They describe switchings between a finite set of tasks in a modular fashion. Their strength comes from their ability to create very complex tasks composed of simple tasks, without worrying how the simple tasks are implemented. BTs present some similarities to hierarchical state machines with the key difference that the main building block of a behavior is a task rather than a state. Its ease of human understanding make BTs less error prone and very popular in the game developer community.

Background
BTs originates from the computer game industry as a powerful tool to model the behavior of non-player characters (NPCs).[1][2][3][4] They have been extensively used in high profile video games such as Halo, Bioshock, and Spore. Recent works propose BTs as a multi-mission control framework for UAV, complex robots, robotic manipulation, and multi-robot systems.[5][6][7][8][9][10]
Key concepts
BT is graphically represented as a directed tree in which the nodes are classified as root, control flow nodes, or execution nodes (tasks). For each pair of connected nodes the outgoing node is called parent and the incoming node is called child. The root has no parents and exactly one child, the control flow nodes have one parent and at least one child, and the execution nodes have one parent and no children. Graphically, the children of a control flow node are placed below it, ordered from left to right.[11]
The execution of a BT starts from the root which sends ticks with a certain frequency to its child. A tick is an enabling signal that allows the execution of a child. When the execution of a node in the BT is allowed, it returns to the parent a status running if its execution has not finished yet, success if it has achieved its goal, or failure otherwise.
Control flow node
A control flow node is used to control the subtasks of which it is composed. A control flow node may be either a selector (fallback) node or a sequence node. They run each of their subtasks in turn. When a subtask is completed and returns its status (success or failure), the control flow node decides whether to execute the next subtask or not.
Selector (fallback) node

Fallback nodes are used to find and execute the first child that does not fail. A fallback node will return immediately with a status code of success or running when one of its children returns success or running (see Figure I and the pseudocode below). The children are ticked in order of importance, from left to right.
In pseudocode, the algorithm for a fallback composition is:
1 for i from 1 to n do 2 childstatus ← Tick(child(i)) 3 if childstatus = running 4 return running 5 else if childstatus = success 6 return success 7 end 8 return failure
Sequence node
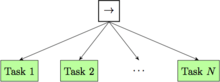
Sequence nodes are used to find and execute the first child that has not yet succeeded. A sequence node will return immediately with a status code of failure or running when one of its children returns failure or running (see Figure II and the pseudocode below). The children are ticked in order, from left to right.
In pseudocode, the algorithm for a sequence composition is:
1 for i from 1 to n do 2 childstatus ← Tick(child(i)) 3 if childstatus = running 4 return running 5 else if childstatus = failure 6 return failure 7 end 8 return success
Mathematical definition
BT are defined as three-tuple.[12]
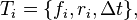
where 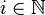 is the index of the tree,
is the index of the tree, 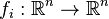 is a vector field representing the right hand side of an ordinary difference equation,
is a vector field representing the right hand side of an ordinary difference equation,  is a time step and
is a time step and
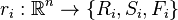 is the return status, that can be equal to either
Running
is the return status, that can be equal to either
Running 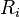 ,
Success
,
Success 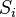 , or
Failure
, or
Failure  .
.
Note: A task is degenerate BT with no parent and no child.
Behavior tree execution
The execution of a BT is described by the following standard ordinary difference equations:
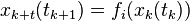
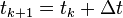
where  represent the discrete time, and
represent the discrete time, and 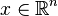 is the state space of the system modelled by the behavior tree.
is the state space of the system modelled by the behavior tree.
Fallback composition
Two BTs 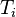 and
and  can be composed into a more complex BT
can be composed into a more complex BT 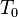 using a Fallback operator.
using a Fallback operator.
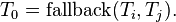
Then return status  and the vector field
and the vector field  associated with
associated with 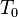 are defined as follows:
are defined as follows:
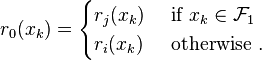
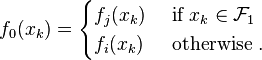
Sequence composition
Two BTs 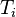 and
and  can be composed into a more complex BT
can be composed into a more complex BT 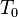 using a Sequence operator.
using a Sequence operator.
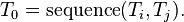
Then return status  and the vector field
and the vector field  associated with
associated with 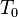 are defined as follows:
are defined as follows:
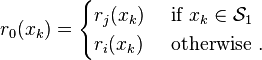
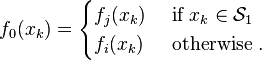
See also
External links
- Behavior Trees for Next-Gen Game AI, video introduction to behavior trees and possible extensions at AiGameDev.com
References
- ↑ Isla D. 2005. Handling complexity in the Halo 2 AI. In Game Developers Conference (Vol. 12)
- ↑ Champandard A. 2007. Understanding BTs. AiGameDev. com, 6
- ↑ Isla D. 2008. Halo 3-building a better battle. In Game Developers Conference. 2008.
- ↑ Lim, C. U., Baumgarten, R., & Colton, S. 2010. Evolving behaviour trees for the commercial game DEFCON. In Applications of Evolutionary Computation, pp. 100-110. Springer Berlin Heidelberg, 2010.
- ↑ Ögren, Petter. "Increasing Modularity of UAV Control Systems using Computer Game BTs." In AIAA Guidance, Navigation and Control Conference, Minneapolis, Minnesota, pp. 13-16. 2012.
- ↑ Colledanchise, Michele, Marzinotto Alejandro, and Ögren Petter."Performance Analysis of Stochastic BTs." In Robotics and Automation (ICRA), 2014 IEEE International Conference on. 2014.
- ↑ Marzinotto, Alejandro, Colledanchise Michele, Smith Christian, and Ögren Petter. "Towards a Unified BTs Framework for Robot Control." In Robotics and Automation (ICRA), 2014 IEEE International Conference on. 2014.
- ↑ Klöckner, Andreas. "Interfacing BTs with the World Using Description Logic." In AIAA Guidance, Navigation and Control Conference, Boston, MA. 2013.
- ↑ Klöckner, Andreas. "Behavior Trees for UAV Mission Management." In GI-Jahrestagung, pp. 57-68. 2013.
- ↑ Bagnell, J. Andrew, Felipe Cavalcanti, Lei Cui, Thomas Galluzzo, Martial Hebert, Moslem Kazemi, Matthew Klingensmith et al. "An integrated system for autonomous robotics manipulation." In Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference on, pp. 2955-2962. IEEE, 2012.
- ↑ craft ai 2015. BT 101 – Behavior Trees grammar basics
- ↑ Colledanchise Michele, and Ögren Petter."How Behavior Trees Modularize Robustness and Safety in Hybrid Systems." In Intelligent Robots and Systems (IROS), 2014 IEEE/RSJ International Conference on, IEEE, 2014.