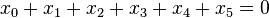Barth–Nieto quintic

In algebraic geometry, the Barth–Nieto quintic is a quintic 3-fold in 4 (or sometimes 5) dimensional projective space studied by Barth & Nieto (1994) that is the Hessian of the Segre cubic. The Barth–Nieto quintic is the closure of the set of points (x₀:x₁:x₂:x₃:x₄:x₅) of P⁵ satisfying the equations

\displaystyle x_0+x_1+x_2+x_3+x_4+x_5= 0

\displaystyle x_0^{-1}+x_1^{-1}+x_2^{-1}+x_3^{-1}+x_4^{-1}+x_5^{-1} = 0.

The Barth–Nieto quintic is not rational, but has a smooth model that is a Calabi–Yau manifold.

References

Barth, W.; Nieto, I. (1994), "Abelian surfaces of type (1,3) and quartic surfaces with 16 skew lines", Journal of Algebraic Geometry 3 (2): 173–222, ISSN 1056-3911, MR 1257320

This article is issued from Wikipedia - version of the Thursday, October 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.