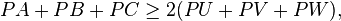Barrow's inequality
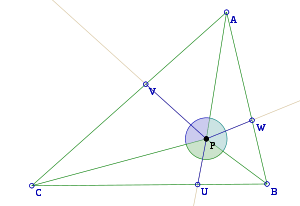
In geometry, Barrow's inequality is an inequality relating the distances between an arbitrary point within a triangle, the vertices of the triangle, and certain points on the sides of the triangle.
Statement
Let P be an arbitrary point inside the triangle ABC. From P and ABC, define U, V, and W as the points where the angle bisectors of BPC, CPA, and APB intersect the sides BC, CA, AB, respectively. Then Barrow's inequality states that
with equality holding only in the case of an equilateral triangle.
History
Barrow's inequality strengthens the Erdős–Mordell inequality, which has identical form except with PU, PV, and PW replaced by the three distances of P from the triangle's sides. It is named after David Francis Barrow. Barrow's proof of this inequality was published in 1937, as his solution to a problem posed in the American Mathematical Monthly of proving the Erdős–Mordell inequality.[1]
A simpler proof was later given by Mordell.[2]
See also
References
- ↑ Erdős, Paul; Mordell, L. J.; Barrow, David F. (1937), "Solution to problem 3740", American Mathematical Monthly 44 (4): 252–254, doi:10.2307/2300713, JSTOR 2300713.
- ↑ Mordell, L. J. (1962), "On geometric problems of Erdös and Oppenheim", Mathematical Gazette 46 (357): 213–215, JSTOR 3614019.