Barotropic fluid

Barotropic fluid stratification of pressure and density

In fluid dynamics, a barotropic fluid is a fluid whose density is a function of pressure only.[1] The barotropic fluid is a useful model of fluid behavior in a wide variety of scientific fields, from meteorology to astrophysics.

The density of most liquids is nearly constant so it can be stated that their densities vary only weakly with pressure and temperature. To a first approximation, liquids are barotropic. To greater precision, they are not barotropic. For example, the density of seawater varies a few percent with temperature and salinity (as well as pressure) so it is not truly barotropic.

In astrophysics, barotropic fluids are important in the study of stellar interiors or of the interstellar medium. One common class of barotropic model used in astrophysics is a polytropic fluid. Typically, the barotropic assumption is not very realistic.

In meteorology, a barotropic atmosphere is one in which the density depends only on pressure, so that isobaric surfaces (constant-pressure surfaces) are also isopycnic surfaces (constant-density surfaces). The isobaric surfaces will also be isothermal surfaces, hence (from the thermal wind equation) the geostrophic wind is independent of height. Hence the motions of a rotating barotropic air mass or fluid are strongly constrained. The tropics are more nearly barotropic than mid-latitudes because temperature is more nearly horizontally uniform in the tropics.

A barotropic flow is a generalization of the barotropic atmosphere. It is a flow in which the pressure is a function of the density only and vice versa. In other words, it is a flow in which isobaric surfaces are isopycnic surfaces and vice versa. One may have a barotropic flow with a non-barotropic fluid, but a barotropic fluid must always follow a barotropic flow. Examples include barotropic layers of the oceans, an isothermal ideal gas or an isentropic ideal gas.

A situation which is not barotropic is baroclinic, i. e., pressure is not enough to specify density. For a barotropic fluid or a barotropic flow (such as a barotropic atmosphere), the baroclinic vector is zero.

See also

References

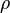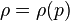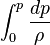  1. ↑ Shames, Irving H. (1962). Mechanics of Fluids. McGraw-Hill. p. 159. LCCN 61018731. Retrieved 8 November 2012. If \rho{} is expressible as a function of p only, that is, \rho = \rho{}(p), the \int_0^p \frac{dp}{\rho{}} in Eq. 5-66 is integrable. Fluids having this characteristic are called barotropic fluids.
This article is issued from Wikipedia - version of the Saturday, December 26, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.