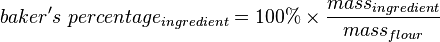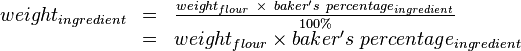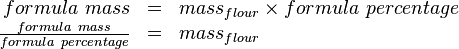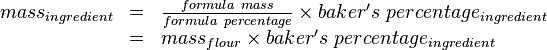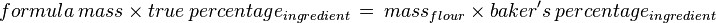Baker percentage

Baker's percentage is a baker's notation method indicating the flour-relative proportion of an ingredient used when making breads, cakes, muffins, and other pastries.[1][2][3][4] It is also referred to as baker's math,[5][6] or otherwise contextually indicated by a phrase such as based on flour weight.[1][7] It is sometimes called formula percentage,[1] a phrase that refers to the sum of a set of bakers' percentages.[note 1] Baker's percentage expresses each ingredient in parts per hundred as a ratio of the ingredient's mass to the total flour's mass (that is, the unit mass):[12][13][10]

baker's\ percentage_{ingredient} = 100\% \times \frac{mass_{ingredient}}{mass_{flour}}

For example, in a recipe that calls for 10 pounds of flour and 5 pounds of water, the corresponding baker's percentages are 100% for the flour and 50% for the water. Because these percentages are stated with respect to the mass of flour rather than with respect to the mass of all ingredients, the total sum of these percentages always exceeds 100%.

Flour-based recipes are more precisely conceived as baker's percentages, and more accurately measured using mass instead of volume. The uncertainty in using volume measurements follows from the fact that flour settles in storage and therefore does not have a constant density.[14][15]

Baker percentages

A yeast-dough formula could call for the following list of ingredients, presented as a series of baker's percentages:

flour  100% 
water 35%
milk† 35%
fresh yeast  4%††
salt 1.8%

Conversions

There are several common conversions that are used with baker's percentages. Converting baker's percentages to ingredient weights is one. Converting known ingredient weights to baker percentages is another. Conversion to true percentages, or based on total weight, is helpful to calculate unknown ingredient weights from a desired total or formula weight.

Using baker percentages

To derive the ingredient weights when any weight of flour (Wf) is chosen:[note 2]

\begin{array}{rcl}weight_{ingredient} &=& \frac{weight_{flour}\ \times \ baker's\ percentage_{ingredient}}{100\%}\\ &=& {weight_{flour} \times baker's\ percentage_{ingredient}}\\\end{array}
Digital scale for weighing ingredients.
Baker's
percentage 		weights
[note 3]
ingredient  % method 1 method 2
flour  100%   Wf * 1.00  Wf * 100%
water 35%  Wf * 0.35  Wf * 35%
milk 35%  Wf * 0.35  Wf * 35%
fresh yeast 4%  Wf * 0.04  Wf * 4%
salt 1.8%  Wf * 0.018   Wf * 1.8%

In the example below, 2 lb and 10 kg of flour weights have been calculated. Depending on the desired weight unit, only one of the following four weight columns is used:

Weighing ingredients.
Baker's
percentage 		weights
2 lb 10 kg
ingredient  % lb oz kg g
flour  100%  2 32 10  10000 
water 35% 0.7 11.2 3.5 3500
milk 35% 0.7 11.2 3.5 3500
fresh yeast 4% 0.08 1.28 0.4 400
salt 1.8%  0.036   0.576   0.18  180

Creating baker's percentages

The baker has determined how much a recipe's ingredients weigh, and uses uniform decimal weight units. All ingredient weights are divided by the flour weight to obtain a ratio, then the ratio is multiplied by 100% to yield the baker's percentage for that ingredient:

Using a balance to measure a mass of flour.
ingredient   weight   ingredient mass⁄flour mass  × 100%
flour 10 kg 10 kg ÷ 10 kg = 1.000 = 100%
water 3.5 kg 3.5 kg ÷ 10 kg = 0.350 = 35%
milk 3.5 kg 3.5 kg ÷ 10 kg = 0.350 = 35%
fresh yeast 0.4 kg 0.4 kg ÷ 10 kg = 0.040 = 4%
salt 0.18 kg 0.18 kg ÷ 10 kg = 0.018 = 1.8%

Due to the canceling of uniform weight units, the baker may employ any desired system of measurement (metric or avoirdupois,[16] etc.) when using a baker's percentage to determine an ingredient's weight. Generally, the baker finds it easiest to use the system of measurement that is present on the available tools.

Formula percentage and total mass

Ingredient
[note 4] 		baker's
% 		true
%
flour  100%   56.88% 
water 35% 19.91%
milk 35% 19.91%
fresh yeast  4% 2.28%
salt 1.8% 1.02%
Total 175.8% 100%

The total or sum of the baker's percentages is called the formula percentage. The sum of the ingredient masses is called the formula mass (or formula "weight"). Here are some interesting calculations:

\begin{array}{rcl}formula\ mass & = & mass_{flour} \times formula\ percentage\\ \frac{formula\ mass}{formula\ percentage} & = & mass_{flour}\\\end{array}
\begin{array}{rcl} mass_{ingredient} & = & formula\ mass \times true\ percentage_{ingredient} \\ true\ percentage_{ingredient} & = & \frac{baker's\ percentage_{ingredient}}{formula\ percentage} \times 100\% \\ mass_{ingredient} & = & formula\ mass \times \frac{baker's\ percentage_{ingredient}}{formula\ percentage} \\ & = & \frac{formula\ mass \ \times\ baker's\ percentage_{ingredient}}{formula\ percentage} \end{array}
Thus, it is not necessary to calculate each ingredient's true percentage in order to calculate each ingredient's mass, provided the formula mass and the baker's percentages are known.
\begin{array}{rcl} mass_{ingredient} & = & \frac{formula\ mass}{formula\ percentage} \times baker's\ percentage_{ingredient}\\ & = & mass_{flour} \times baker's\ percentage_{ingredient}\end{array}
formula\ mass \ \times \ true\ percentage_{ingredient} \ = \ mass_{flour}\ \times\ baker's\ percentage_{ingredient}

Weights and densities

The use of customary U.S. units can sometimes be awkward and the metric system makes these conversions simpler. In the metric system, there are only a small number of basic measures of relevance to cooking: the gram (g) for weight, the liter (L) for volume, the meter (m) for length, and degrees Celsius (°C) for temperature; multiples and sub-multiples are indicated by prefixes, two commonly used metric cooking prefixes are milli- (m-) and kilo- (k-).[17] Intra-metric conversions involve moving the decimal point.[18]

Common avoirdupois and metric weight equivalences:[19]

1 pound (lb) = 16 ounces (oz)
1 kilogram (kg) = 1,000 grams (g) = 2.20462262 lb [note 5]
1 lb = 453.59237 g = 0.45359237 kg
1 oz = 28.3495231 g.

In four different English-language countries of recipe and measuring-utensil markets, approximate cup volumes range from 236.59 to 284.1 milliliters (mL). Adaptation of volumetric recipes can be made with density approximations:

Volume to mass conversions for some common cooking ingredients
ingredient density
g/mL
[note 6]		 metric cup
250 mL		 imperial cup
≈284 mL		 U.S. customary cup
≈237 mL[note 7]
g oz g oz g oz
water[note 8] 1[note 9] 249–250 8.8 283–284 10 236–237 8.3[note 10]
granulated sugar 0.8[20] 200 7.0 230 8.0 190 6.7
wheat flour 0.5–0.6[20] 120–150 4.4–5.3 140–170 5.0–6.0 120–140 4.2–5.0
table salt 1.2[20] 300 10.6 340 12.0 280 10.0

Due to volume and density ambiguities, a different approach involves volumetrically measuring the ingredients, then using scales or balances of appropriate accuracy and error ranges to weigh them, and recording the results. With this method, occasionally an error or outlier of some kind occurs.

Drawbacks

Baker's percentages do not accurately reflect the impact of the amount of gluten-forming proteins in the flour on the final product and therefore may need to be adjusted from country to country, or even miller to miller, depending on definitions of terms like "bread flour" and actual protein content.[21] Manipulation of known flour-protein levels can be calculated with a Pearson square.[22][23]

Digital scale with readability of 0.01 g.

In home baking, the amounts of ingredients such as salt or yeast expressed by mass may be too small to measure accurately on the scales used by most home cooks. For these ingredients, it may be easier to express quantities by volume, based on standard densities. For this reason, many breadmaking books that are targeted to home bakers provide both percentages and volumes for common batch sizes.

Besides the need for appropriate readability scales, a kitchen calculator is helpful when working directly from baker's percentages.

Advantages

Baker's percentages enable the user to:

Common Formulations

Common formulations for bread[24] include 100% flour, 60% water/liquid, 1% yeast, 2% salt and 1% oil, lard or butter.

Dough hydration

In a recipe, the baker's percentage for water is referred to as the "hydration"; it is indicative of the stickiness of the dough and the "crumb" of the bread. Lower hydration rates (e.g., 50–57%) are typical for bagels and pretzels, and medium hydration levels (58–65%) are typical for breads and rolls.[25] Higher hydration levels are used to produce more and larger holes, as is common in artisan breads such as baguettes or Ciabatta. Doughs are also often classified by the terms stiff, firm, soft, and slack.[26] Batters are more liquid doughs. Muffins are a type of drop batter while pancakes are a type of pour batter.

Doughs
[25][26]
Very stiff< 57%
Stiff to firm57-65%
Soft 65-70%
Soft to slack 70-80%
Batters
[note 11]
Drop 95%
Pour 190%

Errata

† Except for creams and custards,[27] when the formula includes milk,[28] bakers almost always use high-heat NFDM (non-fat dry milk).[27][29][30][31][32] In breads the usage is typically within a range of 5%-12%; fresh whole milk is 3.5% milk fat, 88% water, and 8.5% milk solids.[29]
†† A yeast flavor in the baked bread is generally not noticeable when the bakers' percent of added yeast is less than 2.5%.[7]

Notes

  1. ↑ There is some ambiguity regarding the use of the phrase "formula percentage" in the literature. From the published date of 2004[8] to the date 2007,[9] Hui's definitions have changed slightly. In 2004 "formula percent" was defined by "total weight of all ingredients"; however by the latter date's usage, the preference was to use the prefix "true" in the phrase "True formula percent (true percent)" when referring to "total weight of all ingredients." In 2005, Ramaswamy & Marcotte used the phrase "typical formula" in reference to a "baker's %" series of ingredients, then drew the semantic and mathematic distinctions that "actual percentage" was one based upon "total mass", which they labeled "% flour", "% water", etc.[10] In 2010, Figoni said that "baker's percentage" was "sometimes called formula percentage...."[1] In 1939, the phrase formula percentage was said to commonly refer to the sum of the particular percentages that would later be called bakers' percentages.[11]
  2. ↑ Derived algebraically from Gisslen's formula.
  3. ↑ Wf denotes a flour weight. In method 1 the percentage was divided by 100%. Method 2 works well when using a calculator. When using a spreadsheet, formatting the cell as percentage versus number automatically handles the per-cent portion of the calculation.
  4. ↑ True percentage values have been rounded and are approximate.
  5. ↑ It's worth noting the multiplicative inverse of 2.20462262.
  6. ↑ One gram per millilitre is very close to one avoirdupois ounce per fluid ounce: 1 g/mL ≈ 1.002 av oz/imp fl oz This is not a numerical coincidence, but comes from the original definition of the kilogram as the mass of one litre of water, and the imperial gallon as the volume occupied by ten avoirdupois pounds of water. The slight difference is due to water at 4 °C (39 °F) being used for the kilogram, and at 62 °F (17 °C) for the imperial gallon. The U.S. fluid ounce is slightly larger.
    1 g/mL ≈ 1.043 av oz/U.S. fl oz
  7. ↑ From cup (unit). Note the similarity of cup mL to water weight or mass as g. This density relationship can also be useful for determining unknown volumes.
  8. ↑ 1 g/mL is a good rough guide for water-based liquids such as milk (the density of milk is about 1.03–1.04 g/mL).
  9. ↑ The density of water ranges from about 0.96 to 1.00 g/mL dependent on temperature and pressure. The table above assumes a temperature range 0–30 °C (32–86 °F). The variation is too small to make any difference in cooking.
  10. ↑ Since an imperial cup of water weighs approximately 10 avoirdupois ounces and five imperial cups are approximately equal to six U.S. cups, one U.S. cup of water weighs approximately 8⅓ avoirdupois ounces.
  11. ↑ Mathematically converted from liquid-to-dry volumetric ratios on quick bread. 1 cup water weighs 237 g, 1 cup all purpose flour, 125 g, rounding applied. It is worth noting that if the liquid is whole milk of 3.25% milkfat, which is somewhat common in pancake recipes, the actual water content or hydration is about 88% of that value per the USDA National Nutrient database, thus pancake hydrations may be as low as, or lower than, 167% or thereabouts (190% * 88%).

References

  1. 1 2 3 4 Paula I. Figoni (2010). How Baking Works: Exploring the Fundamentals of Baking Science. New York: Wiley. pp. 9–11. ISBN 0-470-39267-3. Retrieved 2010-12-06. Baker's percentage—sometimes called formula percentage or indicated as "on flour weight basis"—is different from the percentages commonly taught in math classes.
  2. 1 2 Griffin, Mary Annarose; Gisslen, Wayne (2005). Professional baking (4th ed.). New York: John Wiley. p. 10. ISBN 0-471-46427-9. Retrieved 2011-01-01.
  3. 1 2 Corriher, Shirley (2008). BakeWise: The Hows and Whys of Successful Baking with Over 200 Magnificent Recipes. New York: Scribner. p. 32. ISBN 1-4165-6078-5. Retrieved 2010-12-09.
  4. ↑ Hui, Yiu H. (2006). Handbook of food science, technology, and engineering. Washington, DC: Taylor & Francis. p. 16-6. ISBN 0-8493-9849-5. Retrieved 2010-12-09.
  5. ↑ Laura Halpin Rinsky; Glenn Rinsky (2009). The pastry chef's companion: a comprehensive resource guide for the baking and pastry professional. Chichester: John Wiley & Sons. p. 19. ISBN 0-470-00955-1. Retrieved 2010-12-09.
  6. ↑ Daniel T. DiMuzio (2009). Bread Baking: An Artisan's Perspective. New York: Wiley. p. 31. ISBN 0-470-13882-3. Retrieved 2010-12-11.
  7. 1 2 Cauvain, Stanley P. (2003). Bread making: improving quality. Boca Raton: CRC Press. p. 475. ISBN 1-85573-553-9. Retrieved 2010-12-08. Generally the taste of yeast itself is not detectable in bread unless the amount of yeast used is greater than 2.5% based on the weight of flour.
  8. ↑ J. Scott Smith, Yiu H. Hui, ed. (2004). Food processing: principles and applications. Cambridge, MA: Blackwell Pub. p. 178. ISBN 0-8138-1942-3. Retrieved 2010-12-29. Formula—term used instead of "recipe," by the baking industry; the weight of each ingredient is determined based on the weight of flour at 100%.
    Formula percent—term used by the baking industry to describe the amount of each ingredient by weight for a "recipe" or formula compared to the weight of all ingredients.
  9. ↑ Yiu H. Hui, ed. (2007). Handbook of food products manufacturing. New York: Wiley. p. 302. ISBN 0-470-12524-1. Retrieved 2010-12-29. True formula percent (true percent): Term used by the baking industry to describe the amount of each ingredient by weight for a "recipe" or formula compared with the total weight of all ingredients.
  10. 1 2 3 Michele Marcotte; Hosahalli Ramaswamy (2005). Food Processing: Principles and Applications. Boca Raton: CRC. pp. 14–15. ISBN 1-58716-008-0. Retrieved 2010-12-25.
  11. 1 2 Quartermaster Corps, ed. (1939). Army baker. Washington: U.S. Government Printing Office. pp. 38–41. Training Manual No. 2100-151. Retrieved 2012-02-07. The sum of the percentages of ingredients used in any dough is commonly referred to as the formula percentage (168 percent in example in b above). The sum of the weights of ingredients used in a dough is commonly referred to as formula weight (462 pounds in example in c above).
  12. ↑ Gisslen, Wayne (2007). Professional cooking (Sixth ed.). New York: John Wiley. p. 893. ISBN 0-471-66376-X. Retrieved 2010-12-25.
  13. ↑ Gisslen, Wayne (2009). Professional baking. New York: John Wiley. p. 24. ISBN 0-471-78349-8.
  14. ↑ Stanley P Cauvain (2009). Stanley P. Cauvain & Linda S. Young, ed. The ICC Handbook of Cereals, Flour, Dough & Product Testing: Methods and Applications. BakeTran, High Wycombe, Buckinghamshire, UK. Lancaster, Pennsylvania: DEStech Publications, Inc. p. 69. ISBN 1-932078-99-1. Retrieved 2010-12-26. Using Cereal Testing at Mill Intake" > "The Bulk Density of Grain (Hectolitre Mass, Bushel Mass, Test Weight, Specific Weight)
  15. ↑ Wihlfahrt, Julius Emil (1913) [1905]. A treatise on flour, yeast, fermentation and baking, together with recipes for bread and cakes. THE FLEISCHMANN CO. p. 25. Retrieved 2010-01-22.
  16. ↑ Rees, Nicole; Amendola, Joseph (2003). The baker's manual: 150 master formulas for baking. London: J. Wiley. p. 11. ISBN 0-471-40525-6. Retrieved 2010-12-06.
  17. ↑ "The Metric Kitchen". Retrieved 2010-11-30.
  18. ↑ "Intra-metric Conversions" (Doc). Retrieved 2011-02-15.
  19. ↑ Google Calculator, retrieved 2010-12-18
  20. 1 2 3 L. Fulton, E. Matthews, C. Davis: Average weight of a measured cup of various foods. Home Economics Research Report No. 41, Agricultural Research Service, United States Department of Agriculture, Washington, DC, 1977.
  21. ↑ "KitchenSavvy: Flour Power?". Retrieved 2010-12-09.
  22. ↑ Hosahalli Ramaswamy; Amalendu Chakraverty; Mujumdar, Arun S.; Vijaya Raghavan (2003). Handbook of postharvest technology: cereals, fruits, vegetables, tea, and spices. New York, N.Y: Marcel Dekker. p. 263. ISBN 0-8247-0514-9. Retrieved 2010-01-07.
  23. ↑ Van Loon, Dirk (1976). The family cow. Charlotte, Vt: Garden Way Pub. p. 152. ISBN 0-88266-066-7.
  24. ↑ Reinhart, Peter (2009). Peter Reinhart's Artisan Breads Every Day. Berkeley, Calif: Ten Speed Press. pp. 207–209. ISBN 1-58008-998-4. Retrieved 2010-12-09.
  25. 1 2 http://www.stellaculinary.com/scs20
  26. 1 2 "Bakers Percentages - Revised" (HTML). Retrieved 2014-11-28.
  27. 1 2 Paula I. Figoni (2010). How Baking Works: Exploring the Fundamentals of Baking Science. New York: Wiley. p. 360. ISBN 0-470-39267-3. Retrieved 2010-12-08.
  28. ↑ Schieberle, Peter (2009). Food Chemistry. Berlin: Springer. p. 716. ISBN 3-540-69933-3. Retrieved 2010-12-11.
  29. 1 2 Hui, Yiu H. (2006). Handbook of food science, technology, and engineering. Washington, DC: Taylor & Francis. p. 148-26. ISBN 0-8493-9849-5. Retrieved 2010-12-08.
  30. ↑ Mark Keeney; Jenness, Robert; Marth, Elmer H.; Noble P. Wong (1988). Fundamentals of Dairy Chemistry. Berlin: Springer. p. 760. ISBN 0-8342-1360-5. Retrieved 2010-12-08.
  31. ↑ Daniel T. DiMuzio (2009). Bread Baking: An Artisan's Perspective. New York: Wiley. p. 24. ISBN 0-470-13882-3. Retrieved 2010-12-11.
  32. ↑ Paula I. Figoni (2010). How Baking Works: Exploring the Fundamentals of Baking Science. New York: Wiley. p. 150. ISBN 0-470-39267-3. Retrieved 2010-12-11.

External links

This article is issued from Wikipedia - version of the Friday, July 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.