Bagnold number

The Bagnold number (Ba) is the ratio of grain collision stresses to viscous fluid stresses in a granular flow with interstitial Newtonian fluid, first identified by Ralph Alger Bagnold.[1]

The Bagnold number is defined by

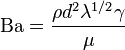\mathrm{Ba}=\frac{\rho d^2 \lambda^{1/2} \gamma}{\mu},[2]

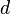where \rho is the particle density, d is the grain diameter, \dot{\gamma} is the shear rate and \mu is the dynamic viscosity of the interstitial fluid. The parameter \lambda is known as the linear concentration, and is given by

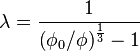\lambda=\frac{1}{\left(\phi_0 / \phi\right)^{\frac{1}{3}} - 1},

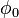where \phi is the solids fraction and \phi_0 is the maximum possible concentration (see random close packing).

In flows with small Bagnold numbers (Ba < 40), viscous fluid stresses dominate grain collision stresses, and the flow is said to be in the 'macro-viscous' regime. Grain collision stresses dominate at large Bagnold number (Ba > 450), which is known as the 'grain-inertia' regime. A transitional regime falls between these two values.

See also

References

  1. ↑ Bagnold, R. A. (1954). "Experiments on a Gravity-Free Dispersion of Large Solid Spheres in a Newtonian Fluid under Shear". Proc. R. Soc. Lond. A 225 (1160): 49–63. doi:10.1098/rspa.1954.0186.
  2. ↑ Hunt, M. L.; Zenit, R.; Campbell, C. S.; Brennen, C.E. (2002). "Revisiting the 1954 suspension experiments of R. A. Bagnold". Journal of Fluid Mechanics (Cambridge University Press) 452: 1–24. doi:10.1017/S0022112001006577.

External links

This article is issued from Wikipedia - version of the Sunday, February 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.