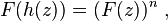Böttcher's equation
Böttcher's equation, named after Lucjan Böttcher, is the functional equation
where
- h is a given analytic function with a superattracting fixed point of order n at a, (that is,
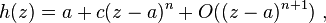 in a neighbourhood of a), with n ≥ 2
in a neighbourhood of a), with n ≥ 2 - F is a sought function.
The logarithm of this functional equation amounts to Schröder's equation.
Solution
Lucian Emil Böttcher sketched a proof in 1904 on the existence of an analytic solution F in a neighborhood of the fixed point a, such that F(a) = 0.[1] This solution is sometimes called the Böttcher coordinate. (The complete proof was published by Joseph Ritt in 1920,[2] who was unaware of the original formulation.[3])
Böttcher's coordinate (the logarithm of the Schröder function) conjugates h(z) in a neighbourhood of the fixed point to the function zn. An especially important case is when h(z) is a polynomial of degree n, and a = ∞ .[4]
Applications
Böttcher's equation plays a fundamental role in the part of holomorphic dynamics which studies iteration of polynomials of one complex variable.
Global properties of the Böttcher coordinate were studied by Fatou [5] and Douady and Hubbard .[6]
See also
References
- ↑ Böttcher, L. E. (1904). "The principal laws of convergence of iterates and their application to analysis (in Russian)". Izv. Kazan. Fiz.-Mat. Obshch. 14: 155–234.
- ↑ Ritt, Joseph (1920). "On the iteration of rational functions". Trans. Amer. Math. Soc 21 (3): 348–356. doi:10.1090/S0002-9947-1920-1501149-6.
- ↑ Stawiska, Małgorzata (November 15, 2013). "Lucjan Emil Böttcher (1872–1937) - The Polish Pioneer of Holomorphic Dynamics". arXiv:1307.7778 [math.HO].
- ↑ Cowen, C. C. (1982). "Analytic solutions of Böttcher's functional equation in the unit disk". Aequationes Mathematicae 24: 187–194. doi:10.1007/BF02193043.
- ↑ Fatou, P. (1919). "Sur les équations fonctionnelles, I". Bulletin de la Société Mathématique de France 47: 161–271. JFM 47.0921.02.; Fatou, P. (1920). "Sur les équations fonctionnelles, II". Bulletin de la Société Mathématique de France 48: 33–94. JFM 47.0921.02.; Fatou, P. (1920). "Sur les équations fonctionnelles, III". Bulletin de la Société Mathématique de France 48: 208–314. JFM 47.0921.02.
- ↑ Douady, A.; Hubbard, J. (1984). "Étude dynamique de polynômes complexes (première partie)". Publ. Math. Orsay.; Douady, A.; Hubbard, J. (1985). "Étude dynamique des polynômes convexes (deuxième partie)". Publ. Math. Orsay.