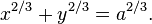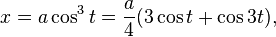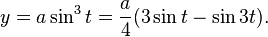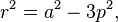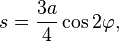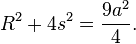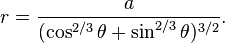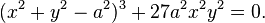Astroid

Not to be confused with asteroid.

Astroid

The hypocycloid construction of the astroid.

An astroid is a particular mathematical curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius.^[1] By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment with an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes.

Its modern name comes from the Greek word for "star". The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse.

Equations

If the radius of the fixed circle is a then the equation is given by^[2]

x^{2/3} + y^{2/3} = a^{2/3}. \,

This implies that an astroid is also a superellipse.

Parametric equations are

x=a\cos^3 t = {a \over 4}( 3\cos t + \cos 3t),

y=a\sin^3 t = {a \over 4}( 3\sin t - \sin 3t).

The pedal equation with respect to the origin is

r^2 = a^2 - 3p^2,

the Whewell equation is

s = {3a \over 4} \cos 2\varphi,

and the Cesàro equation is

R^2 + 4s^2 = \frac{9a^2}{4}.

The polar equation is^[3]

r=\frac{a}{(\cos^{2/3}\theta+\sin^{2/3}\theta)^{3/2}}.

The astroid is a real locus of a plane algebraic curve of genus zero. It has the equation

(x^2+y^2-a^2)^3+27a^2x^2y^2=0. \,

The astroid is therefore a real algebraic curve of degree six.

Metric properties

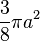
Area enclosed^[4]: $\frac{3}{8} \pi a^2$

Length of curve: $6a$

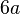
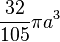
Volume of the surface of revolution of the enclose area about the x-axis.: $\frac{32}{105}\pi a^3$

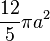
Area of surface of revolution about the x-axis: $\frac{12}{5}\pi a^2$

Properties

The astroid has four cusp singularities in the real plane, the points on the star. It has two more complex cusp singularities at infinity, and four complex double points, for a total of ten singularities.

The dual curve to the astroid is the cruciform curve with equation 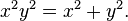$\textstyle x^2 y^2 = x^2 + y^2.$ The evolute of an astroid is an astroid twice as large.

References

↑ Yates
↑ Yates, for section
↑ Mathworld
↑ Yates, for section

J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 4–5,34–35,173–174. ISBN 0-486-60288-5.
Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 10–11. ISBN 0-14-011813-6.
R.C. Yates (1952). "Astroid". A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. pp. 1 ff.

External links

Wikimedia Commons has media related to Astroid.

Hazewinkel, Michiel, ed. (2001), "Astroid", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Weisstein, Eric W., "Astroid", MathWorld.
"Astroid" at The MacTutor History of Mathematics archive
"Astroïde" at Encyclopédie des Formes Mathématiques Remarquables (in French)
Article on 2dcurves.com
Visual Dictionary Of Special Plane Curves, Xah Lee
Bars of an Astroid by Sándor Kabai, The Wolfram Demonstrations Project.

This article is issued from Wikipedia - version of the Saturday, August 01, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Astroid

Equations

Metric properties

Properties

See also

References

External links