Associated prime

In abstract algebra, an associated prime of a module M over a ring R is a type of prime ideal of R that arises as an annihilator of a (prime) submodule of M. The set of associated primes is usually denoted by $\operatorname{Ass}_R(M)\,$ .

In commutative algebra, associated primes are linked to the Lasker-Noether primary decomposition of ideals in commutative Noetherian rings. Specifically, if an ideal J is decomposed as a finite intersection of primary ideals, the radicals of these primary ideals are prime ideals, and this set of prime ideals coincides with 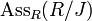$\operatorname{Ass}_R(R/J)\,$ .^[1] Also linked with the concept of "associated primes" of the ideal are the notions of isolated primes and embedded primes.

Definitions

A nonzero R module N is called a prime module if the annihilator $\mathrm{Ann}_R(N)=\mathrm{Ann}_R(N')\,$ for any nonzero submodule N' of N. For a prime module N, $\mathrm{Ann}_R(N)\,$ is a prime ideal in R.^[2]

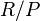An associated prime of an R module M is an ideal of the form $\mathrm{Ann}_R(N)\,$ where N is a prime submodule of M. In commutative algebra the usual definition is different, but equivalent:^[3] if R is commutative, an associated prime P of M is a prime ideal of the form $\mathrm{Ann}_R(m)\,$ for a nonzero element m of M or equivalently $R/P$ is isomorphic to a submodule of M.

In a commutative ring R, minimal elements in $\operatorname{Ass}_R(M)$ (with respect to the set-theoretic inclusion) are called isolated primes while the rest of the associated primes (i.e., those properly containing associated primes) are called embedded primes.

A module is called coprimary if xm = 0 for some nonzero m ∈ M implies xⁿM = 0 for some positive integer n. A nonzero finitely generated module M over a commutative Noetherian ring is coprimary if and only if it has exactly one associated prime. A submodule N of M is called P-primary if 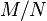$M/N$ is coprimary with P. An ideal I is a P-primary ideal if and only if $\operatorname{Ass}_R(R/I) = \{P\}$ ; thus, the notion is a generalization of a primary ideal.

Properties

Most of these properties and assertions are given in (Lam 2001) starting on page 86.

If M' ⊆M, then 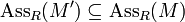$\mathrm{Ass}_R(M')\subseteq\mathrm{Ass}_R(M)\,$ . If in addition M' is an essential submodule of M, their associated primes coincide.
It is possible, even for a commutative local ring, that the set of associated primes of a finitely generated module is empty. However, in any ring satisfying the ascending chain condition on ideals (for example, any right or left Noetherian ring) every nonzero module has at least one associated prime.
Any uniform module has either zero or one associated primes, making uniform modules an example of coprimary modules.
For a one-sided Noetherian ring, there is a surjection from the set of isomorphism classes of indecomposable injective modules onto the spectrum $\mathrm{Spec}(R)\,$ . If R is an Artinian ring, then this map becomes a bijection.
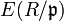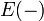Matlis' Theorem: For a commutative Noetherian ring R, the map from the isomorphism classes of indecomposable injective modules to the spectrum is a bijection. Moreover, a complete set of representatives for those classes is given by $E(R/\mathfrak{p})\,$ where $E(-)\,$ denotes the injective hull and $\mathfrak{p}\,$ ranges over the prime ideals of R.
For a Noetherian module M over any ring, there are only finitely many associated primes of M.

The following properties all refer to a commutative Noetherian ring R:

Every ideal J (through primary decomposition) is expressible as a finite intersection of primary ideals. The radical of each of these ideals is a prime ideal, and these primes are exactly the elements of 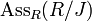$\mathrm{Ass}_R(R/J)\,$ . In particular, an ideal J is a primary ideal if and only if 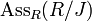$\mathrm{Ass}_R(R/J)\,$ has exactly one element.
Any prime ideal minimal with respect to containing an ideal J is in 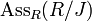$\mathrm{Ass}_R(R/J)\,$ . These primes are precisely the isolated primes.
The set theoretic union of the associated primes of M is exactly the collection of zero-divisors on M, that is, elements r for which there exists nonzero m in M with mr =0.
If M is a finitely generated module over R, then there is a finite ascending sequence of submodules

0=M_0\subset M_1\subset\cdots\subset M_{n-1}\subset M_n=M\,

such that each quotient M_i/M_i−1 is isomorphic to R/P_i for some prime ideals P_i. Moreover every associated prime of M occurs among the set of primes P_i. (In general not all the ideals P_i are associated primes of M.)

Let S be a multiplicatively closed subset of R and 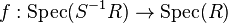$f: \operatorname{Spec}(S^{-1}R) \to \operatorname{Spec}(R)$ the canonical map. Then, for a module M over R,
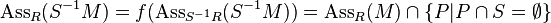$\operatorname{Ass}_R(S^{-1}M) = f(\operatorname{Ass}_{S^{-1}R}(S^{-1}M)) = \operatorname{Ass}_R(M) \cap \{ P | P \cap S = \emptyset \}$ .^[4]
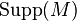For a module M over R, $\mathrm{Ass}(M) \subseteq \mathrm{Supp}(M)$ . Furthermore, the set of minimal elements of $\mathrm{Supp}(M)$ coincides with the set of minimal elements of $\mathrm{Ass}(M)$ . In particular, the equality holds if $\mathrm{Ass}(M)$ consists of maximal ideals.
A module M over R has finite length if and only if M is finitely generated and $\mathrm{Ass}(M)$ consists of maximal ideals.^[5]

Examples

If R is the ring of integers, then non-trivial free abelian groups and non-trivial abelian groups of prime power order are coprimary.
If R is the ring of integers and M a finite abelian group, then the associated primes of M are exactly the primes dividing the order of M.
The group of order 2 is a quotient of the integers Z (considered as a free module over itself), but its associated prime ideal (2) is not an associated prime of Z.

References

↑ Lam 1999, p. 117, Ex 40B.
↑ Lam 1999, p. 85.
↑ Lam 1999, p. 86.
↑ Matsumura 1970, 7.C Lemma
↑ Cohn, P. M. (2003), Basic Algebra, Springer, Exercise 10.9.7, p. 391, ISBN 9780857294289 .

Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1, MR 1322960
Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294
Matsumura, Hideyuki (1970), Commutative algebra

This article is issued from Wikipedia - version of the Wednesday, September 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.