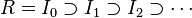Associated graded ring

In mathematics, the associated graded ring of a ring R with respect to a proper ideal I is the graded ring:

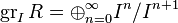\operatorname{gr}_I R = \oplus_{n=0}^\infty I^n/I^{n+1}

Similarly, if M is a left R-module, then the associated graded module is the graded module over $\operatorname{gr}_I R$ :

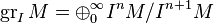\operatorname{gr}_I M = \oplus_0^\infty I^n M/ I^{n+1} M

Basic definitions and properties

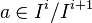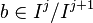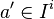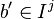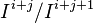For a ring R and ideal I, multiplication in $\operatorname{gr}_IR$ is defined as follows: First, consider homogeneous elements $a \in I^i/I^{i + 1}$ and $b \in I^j/I^{j + 1}$ and suppose $a' \in I^i$ is a representative of a and $b' \in I^j$ is a representative of b. Then define $ab$ to be the equivalence class of $a'b'$ in $I^{i + j}/I^{i + j + 1}$ . Note that this is well-defined modulo 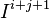$I^{i + j + 1}$ . Multiplication of inhomogeneous elements is defined by using the distributive property.

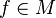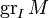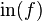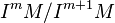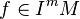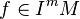A ring or module may be related to its associated graded through the initial form map. Let M be an R-module and I an ideal of R. Given $f \in M$ , the initial form of f in $\operatorname{gr}_I M$ , written $\mathrm{in}(f)$ , is the equivalence class of f in $I^mM/I^{m+1}M$ where m is the maximum integer such that $f\in I^mM$ . If $f \in I^mM$ for every m, then set 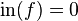$\mathrm{in}(f) = 0$ . The initial form map is only a map of sets and generally not a homomorphism. For a submodule 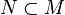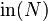$N \subset M$ , $\mathrm{in}(N)$ is defined to be the submodule of 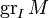$\operatorname{gr}_I M$ generated by 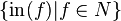$\{\mathrm{in}(f) | f \in N\}$ . This may not be the same as the submodule of 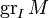$\operatorname{gr}_IM$ generated by the only initial forms of the generators of N.

A ring inherits some "good" properties from its associated graded ring. For example, if R is a noetherian local ring, and $\operatorname{gr}_I R$ is an integral domain, then R is itself an integral domain.^[1]

Examples

Let U be the enveloping algebra of a Lie algebra 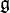$\mathfrak{g}$ over a field k; it is filtered by degree. The Poincaré–Birkhoff–Witt theorem implies that 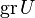$\operatorname{gr} U$ is a polynomial ring; in fact, it is the coordinate ring $k[\mathfrak{g}^*]$ .

The associated graded algebra of a Clifford algebra is an exterior algebra; i.e., a Clifford algebra degenerates to an exterior algebra.

Generalization to multiplicative filtrations

The associated graded can also be defined more generally for multiplicative descending filtrations of R (see also filtered ring.) Let F be a descending chain of ideals of the form

R = I_0 \supset I_1 \supset I_2 \supset \dotsb

such that 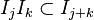$I_jI_k \subset I_{j + k}$ . The graded ring associated with this filtration is 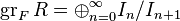$\operatorname{gr}_F R = \oplus_{n=0}^\infty I_n/ I_{n+1}$ . Multiplication and the initial form map are defined as above.

References

↑ Eisenbud, Corollary 5.5

Eisenbud, David (1995). Commutative Algebra. Graduate Texts in Mathematics 150. New York: Springer-Verlag. doi:10.1007/978-1-4612-5350-1. ISBN 0-387-94268-8. MR 1322960.
Matsumura, Hideyuki (1989). Commutative ring theory. Cambridge Studies in Advanced Mathematics 8. Translated from the Japanese by M. Reid (Second ed.). Cambridge: Cambridge University Press. ISBN 0-521-36764-6. MR 1011461.

This article is issued from Wikipedia - version of the Wednesday, September 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Associated graded ring

Basic definitions and properties

Examples

Generalization to multiplicative filtrations

See also

References