Data assimilation

A numerical model determines how a model state at a particular time changes into the model state at a later time. Even if the numerical model were a perfect representation of an actual system (which of course can rarely if ever be the case) in order to make a perfect forecast of the future state of the actual system the initial state of the numerical model would also have to be a perfect representation of the actual state of the system.

Data assimilation or, more-or-less synonymously, data analysis is the process by which observations of the actual system are incorporated into the model state of a numerical model of that system. Applications of data assimilation arise in many fields of geosciences, perhaps most importantly in weather forecasting and hydrology.

A frequently encountered problem is that the number of observations of the actual system available for analysis is orders of magnitude smaller than the number of values required to specify the model state. The initial state of the numerical model cannot therefore be determined from the available observations alone. Instead, the numerical model is used to propagate information from past observations to the current time. This is then combined with current observations of the actual system using a data assimilation method.

Most commonly this leads to the numerical modelling system alternately performing a numerical forecast and a data analysis. This is known as analysis/forecast cycling. The forecast from the previous analysis to the current one is frequently called the background.

The analysis combines the information in the background with that of the current observations, essentially by taking a weighted mean of the two; using estimates of the uncertainty of each to determine their weighting factors. The data assimilation procedure is invariably multivariate and includes approximate relationships between the variables. The observations are of the actual system, rather than of the model's incomplete representation of that system, and so may have different relationships between the variables from those in the model. To reduce the impact of these problems incremental analyses are often performed. That is the analysis procedure determines increments which when added to the background yield the analysis. As the increments are generally small compared to the background values this leaves the analysis less affected by 'balance' errors in the analysed increments. Even so some filtering, known as initialisation, may be required to avoid problems, such as the excitement of unphysical wave like activity or even numerical instability, when running the numerical model from the analysed initial state.

As an alternative to analysis/forecast cycles, data assimilation can proceed by some sort of continuous process such as nudging, where the model equations themselves are modified to add terms that continuously push the model towards the observations.

Data assimilation as statistical estimation

In data assimilation applications, the analysis and forecasts are best thought of as probability distributions. The analysis step is an application of Bayes' theorem and the overall assimilation procedure is an example of recursive Bayesian estimation. However, the probabilistic analysis is usually simplified to a computationally feasible form. Advancing the probability distribution in time would be done exactly in the general case by the Fokker-Planck equation, but that is unrealistically expensive, so various approximations operating on simplified representations of the probability distributions are used instead. If the probability distributions are normal, they can be represented by their mean and covariance, which gives rise to the Kalman filter. However it is not feasible to maintain the covariance because of the large number of degrees of freedom in the state, so various approximations are used instead.

Many methods represent the probability distributions only by the mean and impute some covariance instead. In the basic form, such analysis step is known as optimal statistical interpolation. Adjusting the initial value of the mathematical model instead of changing the state directly at the analysis time is the essence of the variational methods, 3DVAR and 4DVAR. Nudging, also known as Newtonian relaxation or 4DDA, is essentially the same as proceeding in continuous time rather than in discrete analysis cycles (the Kalman-Bucy filter), again with imputing simplified covariance.

Ensemble Kalman filters represent the probability distribution by an ensemble of simulations, and the covariance is approximated by sample covariance.

Weather forecasting applications

Data assimilation is a concept encompassing any method for combining observations of variables such as temperature and atmospheric pressure into models used in numerical weather prediction (NWP).

Two main types of data assimilation (DA) are used: three-dimensional (3DDA) which largely ignores the information present in the temporal distribution of the observations; and four-dimensional (4DDA) which attempts to make use of it.

Why it is necessary

The atmosphere is a fluid. The idea of numerical weather prediction is to sample the state of the fluid at a given time and use the equations of fluid dynamics and thermodynamics to estimate the state of the fluid at some time in the future. The process of entering observation data into the model to generate initial conditions is called initialization. On land, terrain maps available at resolutions down to 1 kilometer (0.6 mi) globally are used to help model atmospheric circulations within regions of rugged topography, in order to better depict features such as downslope winds, mountain waves and related cloudiness that affects incoming solar radiation.[1] The main inputs from country-based weather services are observations from devices (called radiosondes) in weather balloons that measure various atmospheric parameters and transmits them to a fixed receiver, as well as from weather satellites. The World Meteorological Organization acts to standardize the instrumentation, observing practices and timing of these observations worldwide. Stations either report hourly in METAR reports,[2] or every six hours in SYNOP reports.[3] These observations are irregularly spaced, so they are processed by data assimilation and objective analysis methods, which perform quality control and obtain values at locations usable by the model's mathematical algorithms.[4] Some global models use finite differences, in which the world is represented as discrete points on a regularly spaced grid of latitude and longitude;[5] other models use spectral methods that solve for a range of wavelengths. The data are then used in the model as the starting point for a forecast.[6]

A variety of methods are used to gather observational data for use in numerical models. Sites launch radiosondes in weather balloons which rise through the troposphere and well into the stratosphere.[7] Information from weather satellites is used where traditional data sources are not available. Commerce provides pilot reports along aircraft routes[8] and ship reports along shipping routes.[9] Research projects use reconnaissance aircraft to fly in and around weather systems of interest, such as tropical cyclones.[10][11] Reconnaissance aircraft are also flown over the open oceans during the cold season into systems which cause significant uncertainty in forecast guidance, or are expected to be of high impact from three to seven days into the future over the downstream continent.[12] Sea ice began to be initialized in forecast models in 1971.[13] Efforts to involve sea surface temperature in model initialization began in 1972 due to its role in modulating weather in higher latitudes of the Pacific.[14]

History

Lewis Fry Richardson

In 1922, Lewis Fry Richardson published the first attempt at forecasting the weather numerically. Using a hydrostatic variation of Bjerknes's primitive equations,[15] Richardson produced by hand a 6-hour forecast for the state of the atmosphere over two points in central Europe, taking at least six weeks to do so.[16] His forecast calculated that the change in surface pressure would be 145 millibars (4.3 inHg), an unrealistic value incorrect by two orders of magnitude. The large error was caused by an imbalance in the pressure and wind velocity fields used as the initial conditions in his analysis,[15] indicating the need for a data assimilation scheme.

Originally "subjective analysis" had been used in which NWP forecasts had been adjusted by meteorologists using their operational expertise. Then "objective analysis" (e.g. Cressman algorithm) was introduced for automated data assimilation. These objective methods used simple interpolation approaches, and thus were 3DDA methods.

Later, 4DDA methods, called "nudging", were developed, such as in the MM5 model. They are based on the simple idea of Newtonian relaxation (the 2nd axiom of Newton). They introduce into the right part of dynamical equations of the model a term that is proportional to the difference of the calculated meteorological variable and the observed value. This term that has a negative sign keeps the calculated state vector closer to the observations. Nudging can be interpreted as a variant of the Kalman-Bucy filter (a continuous time version of the Kalman filter) with the gain matrix prescribed rather than obtained from covariances.

A major development was achieved by L. Gandin (1963) who introduced the "statistical interpolation" (or "optimal interpolation") method, which developed earlier ideas of Kolmogorov. This is a 3DDA method and is a type of regression analysis which utilizes information about the spatial distributions of covariance functions of the errors of the "first guess" field (previous forecast) and "true field". These functions are never known. However, the different approximations were assumed.

The optimal interpolation algorithm is the reduced version of the Kalman filtering (KF) algorithm and in which the covariance matrices are not calculated from the dynamical equations but are pre-determined in advance.

Attempts to introduce the KF algorithms as a 4DDA tool for NWP models came later. However, this was (and remains) a difficult task because the full version requires solution of the enormous number of additional equations (~N*N~10**12, where N=Nx*Ny*Nz is the size of the state vector, Nx~100, Ny~100, Nz~100 - the dimensions of the computational grid). To overcome this difficulty, approximate or suboptimal Kalman filters were developed. These include the Ensemble Kalman filter and the Reduced-Rank Kalman filters (RRSQRT) (see Todling and Cohn, 1994).

Another significant advance in the development of the 4DDA methods was utilizing the optimal control theory (variational approach) in the works of Le Dimet and Talagrand (1986), based on the previous works of G. Marchuk, who was the first to apply that theory in the environmental modeling. The significant advantage of the variational approaches is that the meteorological fields satisfy the dynamical equations of the NWP model and at the same time they minimize the functional, characterizing their difference from observations. Thus, the problem of constrained minimization is solved. The 3DDA variational methods were developed for the first time by Sasaki (1958).

As was shown by Lorenc (1986), all the above-mentioned 4DDA methods are in some limit equivalent, i.e. under some assumptions they minimize the same cost function. However, in practical applications these assumptions are never fulfilled, the different methods perform differently and generally it is not clear what approach (Kalman filtering or variational) is better. The fundamental questions also arise in application of the advanced DA techniques such as convergence of the computational method to the global minimum of the functional to be minimised. For instance, cost function or the set in which the solution is sought can be not convex. The 4DDA method which is currently most successful[17][18] is hybrid incremental 4D-Var, where an ensemble is used to augment the climatological background error covariances at the start of the data assimilation time window, but the background error covariances are evolved during the time window by a simplified version of the NWP forecast model. This data assimilation method is used operationally at forecast centres such as the Met Office.[19][20]

Cost function

The process of creating the analysis in data assimilation often involves minimization of a cost function. A typical cost function would be the sum of the squared deviations of the analysis values from the observations weighted by the accuracy of the observations, plus the sum of the squared deviations of the forecast fields and the analyzed fields weighted by the accuracy of the forecast. This has the effect of making sure that the analysis does not drift too far away from observations and forecasts that are known to usually be reliable.

3D-Var

J(\mathbf{x}) = (\mathbf{x}-\mathbf{x}_{b})^{\mathrm{T}}\mathbf{B}^{-1}(\mathbf{x}-\mathbf{x}_{b}) + (\mathbf{y}-\mathit{H}[\mathbf{x}])^{\mathrm{T}}\mathbf{R}^{-1}(\mathbf{y}-\mathit{H}[\mathbf{x}]),

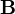where \mathbf{B} denotes the background error covariance, 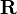\mathbf{R} the observational error covariance.

\nabla J(\mathbf{x}) = 2\mathbf{B}^{-1}(\mathbf{x}-\mathbf{x}_{b}) - 2\mathit{H}^T\mathbf{R}^{-1}(\mathbf{y}-\mathit{H}[\mathbf{x}])

4D-var

J(\mathbf{x}) = (\mathbf{x}-\mathbf{x}_{b})^{\mathrm{T}}\mathbf{B}^{-1}(\mathbf{x}-\mathbf{x}_{b}) + \sum_{i=0}^{n}(\mathbf{y}_{i}-\mathit{H}_{i}[\mathbf{x}_{i}])^{\mathrm{T}}\mathbf{R}_{i}^{-1}(\mathbf{y}_{i}-\mathit{H}_{i}[\mathbf{x}_{i}])

provided that \mathit{H} is linear operator (matrix).

Future development

Factors driving the rapid development of data assimilation methods for NWP models include:

Other applications

Data assimilation methods are currently also used in other environmental forecasting problems, e.g. in hydrological forecasting. Basically, the same types of data assimilation methods as those described above are in use there. An example of chemical data assimilation using Autochem can be found at CDACentral.

Given the abundance of spacecraft data for other planets in the solar system, data assimilation is now also applied beyond the Earth to obtain re-analyses of the atmospheric state of extraterrestrial planets. Mars is the only extraterrestrial planet to which data assimilation has been applied so far. Available spacecraft data include, in particular, retrievals of temperature and dust/water ice optical ticknesses from the Thermal Emission Spectrometer onboard NASA's Mars Global Surveyor and the Mars Climate Sounder onboard NASA's Mars Reconnaissance Orbiter. Two methods of data assimilation have been applied to these datasets: an Analysis Correction scheme [21] and two Ensemble Kalman Filter schemes,[22][23] both using a global circulation model of the martian atmosphere as forward model. The Mars Analysis Correction Data Assimilation (MACDA) dataset is publicly available from the British Atmospheric Data Centre.[24]

Data assimilation is a part of the challenge for every forecasting problem.

Dealing with biased data is a serious challenge in data assimilation. Further development of methods to deal with biases will be of particular use. If there are several instruments observing the same variable then intercomparing them using probability distribution functions can be instructive. Such an analysis is available on line at PDFCentral designed for the validation of observations from the NASA Aura satellite.

Other uses include trajectory estimation for the Apollo program, GPS, and atmospheric chemistry.

Prediction of future oil production

Data assimilation is extensively used in petroleum reservoir engineering, where it is usually referred to as "history matching". Data assimilation methods are used for uncertainty assessment of performance predictions of wells in oil reservoirs,[25] and for generating computational models used for optimizing decision parameters that would improve oil recovery.[26]

References

Footnotes (hyperlinks)

  1. ↑ Stensrud, David J. (2007). Parameterization schemes: keys to understanding numerical weather prediction models. Cambridge University Press. p. 56. ISBN 978-0-521-86540-1. Retrieved 2011-02-15.
  2. ↑ National Climatic Data Center (2008-08-20). "Key to METAR Surface Weather Observations". National Oceanic and Atmospheric Administration. Retrieved 2011-02-11.
  3. ↑ "SYNOP Data Format (FM-12): Surface Synoptic Observations". UNISYS. 2008-05-25. Archived from the original on 2007-12-30.
  4. ↑ Krishnamurti, T. N. (January 1995). "Numerical Weather Prediction". Annual Review of Fluid Mechanics 27 (1): 195–225. Bibcode:1995AnRFM..27..195K. doi:10.1146/annurev.fl.27.010195.001211.
  5. ↑ Kwon, J. H. (2007). Parallel computational fluid dynamics: parallel computings and its applications : proceedings of the Parallel CFD 2006 Conference, Busan city, Korea (May 15–18, 2006). Elsevier. p. 224. ISBN 978-0-444-53035-6. Retrieved 2011-01-06.
  6. ↑ "The WRF Variational Data Assimilation System (WRF-Var)". University Corporation for Atmospheric Research. 2007-08-14. Archived from the original on 2007-08-14.
  7. ↑ Gaffen, Dian J. (2007-06-07). "Radiosonde Observations and Their Use in SPARC-Related Investigations". Archived from the original on 2007-06-07.
  8. ↑ Ballish, Bradley A.; V. Krishna Kumar (November 2008). "Systematic Differences in Aircraft and Radiosonde Temperatures" (PDF). Bulletin of the American Meteorological Society 89 (11): 1689–1708. Bibcode:2008BAMS...89.1689B. doi:10.1175/2008BAMS2332.1. Retrieved 2011-02-16.
  9. ↑ National Data Buoy Center (2009-01-28). "The WMO Voluntary Observing Ships (VOS) Scheme". National Oceanic and Atmospheric Administration. Retrieved 2011-02-15.
  10. ↑ 403rd Wing (2011). "The Hurricane Hunters". 53rd Weather Reconnaissance Squadron. Retrieved 2006-03-30.
  11. ↑ Lee, Christopher (2007-10-08). "Drone, Sensors May Open Path Into Eye of Storm". The Washington Post. Retrieved 2008-02-22.
  12. ↑ National Oceanic and Atmospheric Administration (2010-11-12). "NOAA Dispatches High-Tech Research Plane to Improve Winter Storm Forecasts". Retrieved 2010-12-22.
  13. ↑ Stensrud, David J. (2007). Parameterization schemes: keys to understanding numerical weather prediction models. Cambridge University Press. p. 137. ISBN 978-0-521-86540-1. Retrieved 2011-01-08.
  14. ↑ Houghton, John Theodore (1985). The Global Climate. Cambridge University Press archive. pp. 49–50. ISBN 978-0-521-31256-1. Retrieved 2011-01-08.
  15. 1 2 Lynch, Peter (2008-03-20). "The origins of computer weather prediction and climate modeling" (PDF). Journal of Computational Physics (University of Miami) 227 (7): 3431–44. Bibcode:2008JCoPh.227.3431L. doi:10.1016/j.jcp.2007.02.034. Retrieved 2010-12-23.
  16. ↑ Lynch, Peter (2006). "Weather Prediction by Numerical Process". The Emergence of Numerical Weather Prediction. Cambridge University Press. pp. 1–27. ISBN 978-0-521-85729-1.
  17. ↑ http://ams.confex.com/ams/91Annual/webprogram/Paper181664.html
  18. ↑ http://hfip.psu.edu/EDA2010/MZhang.pdf
  19. ↑ http://www.ecmwf.int/newsevents/meetings/annual_seminar/2011/presentations/Barker.pdf
  20. ↑ http://www.metoffice.gov.uk/research/modelling-systems/unified-model/weather-forecasting
  21. ↑ http://www.atm.ox.ac.uk/group/gpfd/research.html#marsgcm
  22. ↑ http://www.eps.jhu.edu/~mjhoffman/pages/research.html
  23. ↑ http://www.marsclimatecenter.com
  24. ↑ http://badc.nerc.ac.uk/home/
  25. ↑ "History matching production data and uncertainty assessment with an efficient TSVD parameterization algorithm". Journal of Petroleum Science and Engineering 113: 54–71. 2014. doi:10.1016/j.petrol.2013.11.025.
  26. ↑ "Closed-Loop Field Development Optimization Under Uncertainty". SPE Reservoir Simulation Symposium. doi:10.2118/173219-MS.

External links

Examples of how variational assimilation is implemented weather forecasting at:

Other examples of assimilation:

This article is issued from Wikipedia - version of the Friday, October 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.