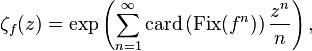Artin–Mazur zeta function

In mathematics, the Artin–Mazur zeta function, named after Michael Artin and Barry Mazur, is a function that is used for studying the iterated functions that occur in dynamical systems and fractals.

It is defined as the formal power series

\zeta_f(z)=\exp \left(\sum_{n=1}^\infty \textrm{card} \left(\textrm{Fix} (f^n)\right) \frac {z^n}{n}\right),

where Fix(ƒ n) is the set of fixed points of the nth iterate of the function ƒ, and card(Fix(ƒ n)) is the cardinality of this set of fixed points.

Note that the zeta function is defined only if the set of fixed points is finite for each n. This definition is formal in that the series does not always have a positive radius of convergence.

The Artin–Mazur zeta function is invariant under topological conjugation.

The Milnor–Thurston theorem states that the Artin–Mazur zeta function is the inverse of the kneading determinant of ƒ.

Analogues

The Artin–Mazur zeta function is formally similar to the local zeta function, when a diffeomorphism on a compact manifold replaces the Frobenius mapping for an algebraic variety over a finite field.

The Ihara zeta function of a graph can be interpreted as an example of the Artin–Mazur zeta function.

See also

References

This article is issued from Wikipedia - version of the Sunday, December 21, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.