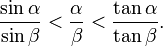Aristarchus' inequality

Aristarchus' inequality (after the Greek astronomer and mathematician Aristarchus of Samos; c. 310 – c. 230 BCE) is a law of trigonometry which states that if α and β are acute angles (i.e. between 0 and a right angle) and β < α then

\frac{\sin\alpha}{\sin\beta} < \frac{\alpha}{\beta} < \frac{\tan\alpha}{\tan\beta}.

Ptolemy used the first of these inequalities while constructing his table of chords.[1]

Notes and references

  1. ↑ Toomer, G. J. (1998), Ptolemy's Almagest, Princeton University Press, p. 54, ISBN 0-691-00260-6

External links


This article is issued from Wikipedia - version of the Sunday, December 06, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.