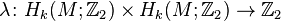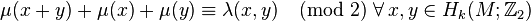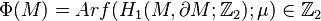Arf invariant

In mathematics, the Arf invariant of a nonsingular quadratic form over a field of characteristic 2 was defined by Turkish mathematician Cahit Arf (1941) when he started the systematic study of quadratic forms over arbitrary fields of characteristic 2. The Arf invariant is the substitute, in characteristic 2, for the discriminant for quadratic forms in characteristic not 2. Arf used his invariant, among others, in his endeavor to classify quadratic forms in characteristic 2.
In the special case of the 2-element field F2 the Arf invariant can be described as the element of F2 that occurs most often among the values of the form. Two nonsingular quadratic forms over F2 are isomorphic if and only if they have the same dimension and the same Arf invariant. This fact was essentially known to Dickson (1901), even for any finite field of characteristic 2, and Arf proved it for an arbitrary perfect field. An assessment of Arf's results in the framework of the theory of quadratic forms can be found in.[1]
The Arf invariant is particularly applied in geometric topology, where it is primarily used to define an invariant of (4k + 2)-dimensional manifolds (singly even-dimensional manifolds: surfaces (2-manifolds), 6-manifolds, 10-manifolds, etc.) with certain additional structure called a framing, and thus the Arf–Kervaire invariant and the Arf invariant of a knot. The Arf invariant is analogous to the signature of a manifold, which is defined for 4k-dimensional manifolds (doubly even-dimensional); this 4-fold periodicity corresponds to the 4-fold periodicity of L-theory. The Arf invariant can also be defined more generally for certain 2k-dimensional manifolds.
Definitions
The Arf invariant is defined for a quadratic form q over a field K of characteristic 2 such that q is nonsingular, in the sense that the associated bilinear form 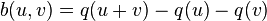 is nondegenerate. The form
is nondegenerate. The form  is alternating since K has characteristic 2; it follows that a nonsingular quadratic form in characteristic 2 must have even dimension. Any binary (2-dimensional) nonsingular quadratic form over K is equivalent to a form
is alternating since K has characteristic 2; it follows that a nonsingular quadratic form in characteristic 2 must have even dimension. Any binary (2-dimensional) nonsingular quadratic form over K is equivalent to a form 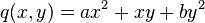 with
with  in K. The Arf invariant is defined to be the product
in K. The Arf invariant is defined to be the product  . If the form
. If the form 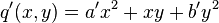 is equivalent to
is equivalent to 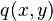 , then the products
, then the products  and
and  differ by an element of the form
differ by an element of the form 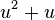 with
with 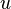 in K. These elements form an additive subgroup U of K. Hence the coset of
in K. These elements form an additive subgroup U of K. Hence the coset of  modulo U is an invariant of
modulo U is an invariant of 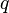 , which means that it is not changed when
, which means that it is not changed when 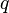 is replaced by an equivalent form.
is replaced by an equivalent form.
Every nonsingular quadratic form 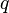 over K is equivalent to a direct sum
over K is equivalent to a direct sum 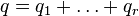 of nonsingular binary forms. This was shown by Arf, but it had been earlier observed by Dickson in the case of finite fields of characteristic 2. The Arf invariant Arf(
of nonsingular binary forms. This was shown by Arf, but it had been earlier observed by Dickson in the case of finite fields of characteristic 2. The Arf invariant Arf(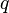 ) is defined to be the sum of the Arf invariants of the
) is defined to be the sum of the Arf invariants of the  . By definition, this is a coset of K modulo U. Arf[2] showed that indeed Arf(
. By definition, this is a coset of K modulo U. Arf[2] showed that indeed Arf(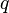 ) does not change if
) does not change if 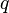 is replaced by an equivalent quadratic form, which is to say that it is an invariant of
is replaced by an equivalent quadratic form, which is to say that it is an invariant of 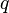 .
.
The Arf invariant is additive; in other words, the Arf invariant of an orthogonal sum of two quadratic forms is the sum of their Arf invariants.
For a field K of characteristic 2, Artin-Schreier theory identifies the quotient group of K by the subgroup U above with the Galois cohomology group H1(K, F2). In other words, the nonzero elements of K/U are in one-to-one correspondence with the separable quadratic extension fields of K. So the Arf invariant of a nonsingular quadratic form over K is either zero or it describes a separable quadratic extension field of K. This is analogous to the discriminant of a nonsingular quadratic form over a field F of characteristic not 2. In that case, the discriminant takes values in F*/(F*)2, which can be identified with H1(F, F2) by Kummer theory.
Arf's main results
If the field K is perfect, then every nonsingular quadratic form over K is uniquely determined (up to equivalence) by its dimension and its Arf invariant. In particular, this holds over the field F2. In this case, the subgroup U above is zero, and hence the Arf invariant is an element of the base field F2; it is either 0 or 1.
If the field K of characteristic 2 is not perfect (that is, K is different from its subfield K2 of squares), then the Clifford algebra is another important invariant of a quadratic form. A corrected version of Arf's original statement is that if the degree [K: K2] is at most 2, then every quadratic form over K is completely characterized by its dimension, its Arf invariant and its Clifford algebra.[3] Examples of such fields are function fields (or power series fields) of one variable over perfect base fields.
Quadratic forms over F2
Over F2, the Arf invariant is 0 if the quadratic form is equivalent to a direct sum of copies of the binary form  , and it is 1 if the form is a direct sum of
, and it is 1 if the form is a direct sum of  with a number of copies of
with a number of copies of  .
.
William Browder has called the Arf invariant the democratic invariant[4] because it is the value which is assumed most often by the quadratic form.[5] Another characterization: q has Arf invariant 0 if and only if the underlying 2k-dimensional vector space over the field F2 has a k-dimensional subspace on which q is identically 0 – that is, a totally isotropic subspace of half the dimension. In other words, a nonsingular quadratic form of dimension 2k has Arf invariant 0 if and only if its isotropy index is k (this is the maximum dimension of a totally isotropic subspace of a nonsingular form).
The Arf invariant in topology
Let M be a compact, connected 2k-dimensional manifold with a boundary  such that the induced morphisms in
such that the induced morphisms in 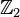 -coefficient homology
-coefficient homology
 ,
, 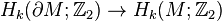
are both zero (e.g. if 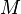 is closed). The intersection form
is closed). The intersection form
is non-singular. (Topologists usually write F2 as 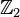 .) A quadratic refinement for
.) A quadratic refinement for  is a function
is a function 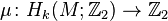 which satisfies
which satisfies
Let 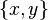 be any 2-dimensional subspace of
be any 2-dimensional subspace of 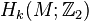 , such that
, such that 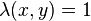 . Then there are two possibilities. Either all of
. Then there are two possibilities. Either all of 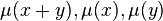 are 1, or else just one of them is 1, and the other two are 0. Call the first case
are 1, or else just one of them is 1, and the other two are 0. Call the first case 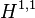 , and the second case
, and the second case 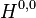 .
Since every form is equivalent to a symplectic form, we can always find subspaces
.
Since every form is equivalent to a symplectic form, we can always find subspaces 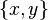 with x and y being
with x and y being  -dual. We can therefore split
-dual. We can therefore split 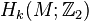 into a direct sum of subspaces isomorphic to either
into a direct sum of subspaces isomorphic to either 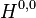 or
or 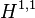 . Furthermore, by a clever change of basis,
. Furthermore, by a clever change of basis, 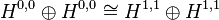 .
We therefore define the Arf invariant
.
We therefore define the Arf invariant
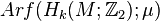 = (number of copies of
= (number of copies of 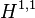 in a decomposition Mod 2)
in a decomposition Mod 2) 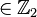 .
.
Examples
- Let
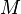 be a compact, connected, oriented 2-dimensional manifold, i.e. a surface, of genus
be a compact, connected, oriented 2-dimensional manifold, i.e. a surface, of genus  such that the boundary
such that the boundary  is either empty or is connected. Embed
is either empty or is connected. Embed 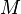 in
in  , where
, where 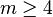 . Choose a framing of M, that is a trivialization of the normal (m-2)-plane vector bundle. (This is possible for
. Choose a framing of M, that is a trivialization of the normal (m-2)-plane vector bundle. (This is possible for 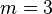 , so is certainly possible for
, so is certainly possible for 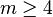 ). Choose a symplectic basis
). Choose a symplectic basis 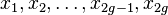 for
for 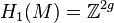 . Each basis element is represented by an embedded circle
. Each basis element is represented by an embedded circle  . The normal (m-1)-plane vector bundle of
. The normal (m-1)-plane vector bundle of  has two trivializations, one determined by a standard framing of a standard embedding
has two trivializations, one determined by a standard framing of a standard embedding  and one determined by the framing of M, which differ by a map
and one determined by the framing of M, which differ by a map 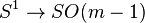 i.e. an element of
i.e. an element of 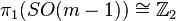 for
for 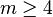 . This can also be viewed as the framed cobordism class of
. This can also be viewed as the framed cobordism class of  with this framing in the 1-dimensional framed cobordism group
with this framing in the 1-dimensional framed cobordism group 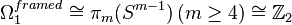 , which is generated by the circle
, which is generated by the circle  with the Lie group framing. The isomorphism here is via the Pontrjagin-Thom construction. Define
with the Lie group framing. The isomorphism here is via the Pontrjagin-Thom construction. Define 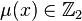 to be this element. The Arf invariant of the framed surface is now defined
to be this element. The Arf invariant of the framed surface is now defined
Note that 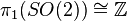 , so we had to stabilise, taking
, so we had to stabilise, taking  to be at least 4, in order to get an element of
to be at least 4, in order to get an element of 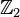 . The case
. The case 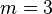 is also admissible as long as we take the residue modulo 2 of the framing.
is also admissible as long as we take the residue modulo 2 of the framing.
- The Arf invariant
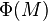 of a framed surface detects whether there is a 3-manifold whose boundary is the given surface which extends the given framing. This is because
of a framed surface detects whether there is a 3-manifold whose boundary is the given surface which extends the given framing. This is because 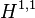 does not bound.
does not bound. 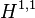 represents a torus
represents a torus  with a trivialisation on both generators of
with a trivialisation on both generators of  which twists an odd number of times. The key fact is that up to homotopy there are two choices of trivialisation of a trivial 3-plane bundle over a circle, corresponding to the two elements of
which twists an odd number of times. The key fact is that up to homotopy there are two choices of trivialisation of a trivial 3-plane bundle over a circle, corresponding to the two elements of 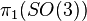 . An odd number of twists, known as the Lie group framing, does not extend across a disc, whilst an even number of twists does. (Note that this corresponds to putting a spin structure on our surface.) Pontrjagin used the Arf invariant of framed surfaces to compute the 2-dimensional framed cobordism group
. An odd number of twists, known as the Lie group framing, does not extend across a disc, whilst an even number of twists does. (Note that this corresponds to putting a spin structure on our surface.) Pontrjagin used the Arf invariant of framed surfaces to compute the 2-dimensional framed cobordism group 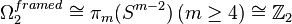 , which is generated by the torus
, which is generated by the torus  with the Lie group framing. The isomorphism here is via the Pontrjagin-Thom construction.
with the Lie group framing. The isomorphism here is via the Pontrjagin-Thom construction. - Let
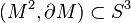 be a Seifert surface for a knot,
be a Seifert surface for a knot, 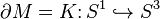 , which can be represented as a disc
, which can be represented as a disc 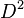 with bands attached. The bands will typically be twisted and knotted. Each band corresponds to a generator
with bands attached. The bands will typically be twisted and knotted. Each band corresponds to a generator 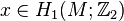 .
.  can be represented by a circle which traverses one of the bands. Define
can be represented by a circle which traverses one of the bands. Define 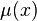 to be the number of full twists in the band modulo 2. Suppose we let
to be the number of full twists in the band modulo 2. Suppose we let 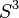 bound
bound  , and push the Seifert surface
, and push the Seifert surface 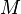 into
into  , so that its boundary still resides in
, so that its boundary still resides in 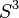 . Around any generator
. Around any generator 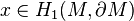 , we now have a trivial normal 3-plane vector bundle. Trivialise it using the trivial framing of the normal bundle to the embedding
, we now have a trivial normal 3-plane vector bundle. Trivialise it using the trivial framing of the normal bundle to the embedding 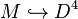 for 2 of the sections required. For the third, choose a section which remains normal to
for 2 of the sections required. For the third, choose a section which remains normal to  , whilst always remaining tangent to
, whilst always remaining tangent to 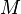 . This trivialisation again determines an element of
. This trivialisation again determines an element of 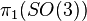 , which we take to be
, which we take to be 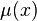 . Note that this coincides with the previous definition of
. Note that this coincides with the previous definition of 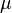 .
. - The Arf invariant of a knot is defined via its Seifert surface. It is independent of the choice of Seifert surface (The basic surgery change of S-equivalence, adding/removing a tube, adds/deletes a
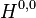 direct summand), and so is a knot invariant. It is additive under connected sum, and vanishes on slice knots, so is a knot concordance invariant.
direct summand), and so is a knot invariant. It is additive under connected sum, and vanishes on slice knots, so is a knot concordance invariant. - The intersection form on the (2k + 1)-dimensional
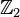 -coefficient homology
-coefficient homology 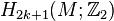 of a framed (4k + 2)-dimensional manifold M has a quadratic refinement
of a framed (4k + 2)-dimensional manifold M has a quadratic refinement 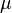 , which depends on the framing. For
, which depends on the framing. For  and
and 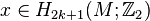 represented by an embedding
represented by an embedding  the value
the value 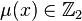 is 0 or 1, according as to the normal bundle of
is 0 or 1, according as to the normal bundle of  is trivial or not. The Kervaire invariant of the framed (4k + 2)-dimensional manifold M is the Arf invariant of the quadratic refinement
is trivial or not. The Kervaire invariant of the framed (4k + 2)-dimensional manifold M is the Arf invariant of the quadratic refinement 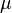 on
on 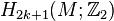 . The Kervaire invariant is a homomorphism
. The Kervaire invariant is a homomorphism 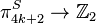 on the (4k + 2)-dimensional stable homotopy group of spheres. The Kervaire invariant can also be defined for a (4k + 2)-dimensional manifold M which is framed except at a point.
on the (4k + 2)-dimensional stable homotopy group of spheres. The Kervaire invariant can also be defined for a (4k + 2)-dimensional manifold M which is framed except at a point. - In surgery theory, for any
 -dimensional normal map
-dimensional normal map 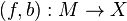 there is defined a nonsingular quadratic form
there is defined a nonsingular quadratic form 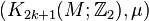 on the
on the 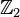 -coefficient homology kernel
-coefficient homology kernel
 refining the homological intersection form
refining the homological intersection form  . The Arf invariant of this form is the Kervaire invariant of (f,b). In the special case
. The Arf invariant of this form is the Kervaire invariant of (f,b). In the special case 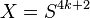 this is the Kervaire invariant of M. The Kervaire invariant features in the classification of exotic spheres by Kervaire and Milnor, and more generally in the classification of manifolds by surgery theory. Browder defined
this is the Kervaire invariant of M. The Kervaire invariant features in the classification of exotic spheres by Kervaire and Milnor, and more generally in the classification of manifolds by surgery theory. Browder defined 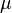 using functional Steenrod squares, and Wall defined
using functional Steenrod squares, and Wall defined 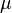 using framed immersions. The quadratic enhancement
using framed immersions. The quadratic enhancement 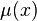 crucially provides more information than
crucially provides more information than  : it is possible to kill x by surgery if and only if
: it is possible to kill x by surgery if and only if 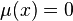 . The corresponding Kervaire invariant detects the surgery obstruction of
. The corresponding Kervaire invariant detects the surgery obstruction of 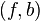 in the L-group
in the L-group 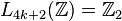 .
.
See also
- de Rham invariant, a mod 2 invariant of (4k + 1)-dimensional manifolds
Notes
References
- See Lickorish (1997) for the relation between the Arf invariant and the Jones polynomial.
- See Chapter 3 of Carter's book for another equivalent definition of the Arf invariant in terms of self-intersections of discs in 4-dimensional space.
- Arf, Cahit (1941), "Untersuchungen über quadratische Formen in Körpern der Charakteristik 2, I", J. Reine Angew. Math 183: 148–167
- Glen Bredon: Topology and Geometry, 1993, ISBN 0-387-97926-3.
- Browder, William (1972), Surgery on simply-connected manifolds, Berlin, New York: Springer-Verlag, MR 0358813
- J. Scott Carter: How Surfaces Intersect in Space, Series on Knots and Everything, 1993, ISBN 981-02-1050-7.
- A.V. Chernavskii (2001), "Arf invariant", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Dickson, Leonard Eugene (1901), Linear groups: With an exposition of the Galois field theory, New York: Dover Publications, MR 0104735
- Kirby, Robion (1989), The topology of 4-manifolds, Lecture Notes in Mathematics 1374, Springer-Verlag, doi:10.1007/BFb0089031, ISBN 0-387-51148-2, MR 1001966
- W. B. Raymond Lickorish, An Introduction to Knot Theory, Graduate Texts in Mathematics, Springer, 1997, ISBN 0-387-98254-X
- Martino, J.; Priddy, S. (2003), "Group Extensions And Automorphism Group Rings", Homology, Homotopy and Applications 5 (1): 53–70, arXiv:0711.1536, doi:10.4310/hha.2003.v5.n1.a3
- L. Pontrjagin, Smooth manifolds and their applications in homotopy theory American Mathematical Society Translations, Ser. 2, Vol. 11, pp. 1–114 (1959)
Further reading
- Lorenz, Falko; Roquette, Peter (2013), "Cahit Arf and his invariant", Contributions to the history of number theory in the 20th century (PDF), Heritage of European Mathematics, Zürich: European Mathematical Society, pp. 189–222, ISBN 978-3-03719-113-2, MR 2934052, Zbl 1276.11001
- Knus, Max-Albert (1991), Quadratic and Hermitian forms over rings, Grundlehren der Mathematischen Wissenschaften 294, Berlin: Springer-Verlag, pp. 211–222, ISBN 3-540-52117-8, MR 1096299, Zbl 0756.11008