Archimedean solid


The truncated icosidodecahedron, is the largest Archimedean solid, by volume with unit edge length, as well as having the most vertices and edges.
The pseudo-rhombicuboctahedron has a single vertex figure, 3.4.4.4, but with a twist on one square cupola. Unlike the (untwisted) rhombicuboctahedron it is not vertex transitive.

In geometry, an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices. They are distinct from the Platonic solids, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

"Identical vertices" are usually taken to mean that for any two vertices, there must be an isometry of the entire solid that takes one vertex to the other. Sometimes it is instead only required that the faces that meet at one vertex are related isometrically to the faces that meet at the other. This difference in definitions controls whether the elongated square gyrobicupola (pseudo-rhombicuboctahedron) is considered an Archimedean solid or a Johnson solid: it is the unique convex polyhedron that has regular polygons meeting in the same way at each vertex, but that does not have a global symmetry taking every vertex to every other vertex. Based on its existence, Branko Grünbaum (2009) has suggested a terminological distinction in which an Archimedean solid is defined as having the same vertex figure at each vertex (including the elongated square gyrobicupola) while a uniform polyhedron is defined as having each vertex symmetric to each other vertex (excluding the gyrobicupola).

Prisms and antiprisms, whose symmetry groups are the dihedral groups, are generally not considered to be Archimedean solids, despite meeting the above definition. With this restriction, there are only finitely many Archimedean solids. All but the elongated square gyrobicupola can be made via Wythoff constructions from the Platonic solids with tetrahedral, octahedral and icosahedral symmetry.

Origin of name

The Archimedean solids take their name from Archimedes, who discussed them in a now-lost work. Pappus refers to it, stating that Archimedes listed 13 polyhedra.[1] During the Renaissance, artists and mathematicians valued pure forms and rediscovered all of these forms. This search was almost entirely completed around 1620 by Johannes Kepler,[2] who defined prisms, antiprisms, and the non-convex solids known as the Kepler-Poinsot polyhedra.

Kepler may have also found the elongated square gyrobicupola (pseudorhombicuboctahedron): at least, he once stated that there were 14 Archimedean solids. However, his published enumeration only includes the 13 uniform polyhedra, and the first clear statement of the pseudorhombicuboctahedron's existence was made in 1905, by Duncan Sommerville.[1]

Classification

There are 13 Archimedean solids (not counting the elongated square gyrobicupola; 15 if the mirror images of two enantiomorphs, see below, are counted separately).

Here the vertex configuration refers to the type of regular polygons that meet at any given vertex. For example, a vertex configuration of (4,6,8) means that a square, hexagon, and octagon meet at a vertex (with the order taken to be clockwise around the vertex).

Name
(Alternative name)		 Schläfli
Coxeter		 Transparent Solid Net Vertex
figure		 Faces Edges Vert. Volume
(unit edges)		 Point
group
truncated tetrahedron{3,3}
(Animation)		 3.6.6
 8 4 triangles
4 hexagons		 18 12 2.710576 Td
cuboctahedron
(rhombitetratetrahedron)		r{4,3} or rr{3,3}
or
(Animation)		 3.4.3.4
 14 8 triangles
6 squares		 24 12 2.357023 Oh
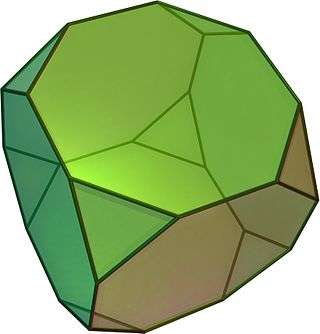
truncated cubet{4,3}
(Animation)		 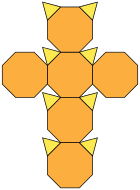3.8.8
 14 8 triangles
6 octagons		 36 24 13.599663 Oh
truncated octahedron
(truncated tetratetrahedron)		t{3,4} or tr{3,3}
or

(Animation)

 4.6.6
 14 6 squares
8 hexagons		 36 24 11.313709 Oh
rhombicuboctahedron
(small rhombicuboctahedron)		rr{4,3}
(Animation)		 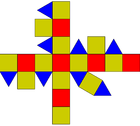3.4.4.4
 26 8 triangles
18 squares		 48 24 8.714045 Oh
truncated cuboctahedron
(great rhombicuboctahedron)		tr{4,3}
(Animation)		 4.6.8
 26 12 squares
8 hexagons
6 octagons		 72 48 41.798990 Oh
snub cube
(snub cuboctahedron)		sr{4,3}
(Animation)		 3.3.3.3.4
 38 32 triangles
6 squares		 60 24 7.889295 O
icosidodecahedronr{5,3}
(Animation)		 3.5.3.5
 32 20 triangles
12 pentagons		 60 30 13.835526 Ih
truncated dodecahedront{5,3}
(Animation)		 3.10.10
 32 20 triangles
12 decagons		 90 60 85.039665 Ih
truncated icosahedront{3,5}
(Animation)		 5.6.6
 32 12 pentagons
20 hexagons		 90 60 55.287731 Ih
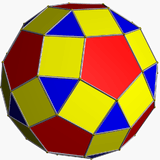
rhombicosidodecahedron
(small rhombicosidodecahedron)		rr{5,3}
(Animation)		 3.4.5.4
 62 20 triangles
30 squares
12 pentagons		 120 60 41.615324 Ih
truncated icosidodecahedron
(great rhombicosidodecahedron)		tr{5,3}
(Animation)		 4.6.10
 62 30 squares
20 hexagons
12 decagons		 180 120 206.803399 Ih
snub dodecahedron
(snub icosidodecahedron)		sr{5,3}
(Animation)		 3.3.3.3.5
 92 80 triangles
12 pentagons		 150 60 37.616650 I

Some definitions of semiregular polyhedron include one more figure, the elongated square gyrobicupola or "pseudo-rhombicuboctahedron".[3]

Properties

The number of vertices is 720° divided by the vertex angle defect.

The cuboctahedron and icosidodecahedron are edge-uniform and are called quasi-regular.

The duals of the Archimedean solids are called the Catalan solids. Together with the bipyramids and trapezohedra, these are the face-uniform solids with regular vertices.

Chirality

The snub cube and snub dodecahedron are known as chiral, as they come in a left-handed (Latin: levomorph or laevomorph) form and right-handed (Latin: dextromorph) form. When something comes in multiple forms which are each other's three-dimensional mirror image, these forms may be called enantiomorphs. (This nomenclature is also used for the forms of certain chemical compounds).

Construction of Archimedean solids

The Archimedean solids can be constructed as generator positions in a kaleidoscope.

The different Archimedean and Platonic solids can be related to each other using a handful of general constructions. Starting with a Platonic solid, truncation involves cutting away of corners. To preserve symmetry, the cut is in a plane perpendicular to the line joining a corner to the center of the polyhedron and is the same for all corners. Depending on how much is truncated (see table below), different Platonic and Archimedean (and other) solids can be created. Expansion or cantellation involves moving each face away from the center (by the same distance so as to preserve the symmetry of the Platonic solid) and taking the convex hull. Expansion with twisting also involves rotating the faces, thus breaking the rectangles corresponding to edges into triangles. The last construction we use here is truncation of both corners and edges. Ignoring scaling, expansion can also be viewed as truncation of corners and edges but with a particular ratio between corner and edge truncation.

Construction of Archimedean Solids
Symmetry Tetrahedral
 Octahedral
 Icosahedral
Starting solid
Operation		Symbol
{p,q}
 Tetrahedron
{3,3}
 Cube
{4,3}
 Octahedron
{3,4}
 Dodecahedron
{5,3}
 Icosahedron
{3,5}
Truncation (t)t{p,q}
 truncated tetrahedron
 truncated cube
 truncated octahedron
 truncated dodecahedron
 truncated icosahedron
Rectification (r)
Ambo (a)		r{p,q}
 tetratetrahedron
 cuboctahedron
 icosidodecahedron
Bitruncation (2t)
Dual kis (dk)		2t{p,q}
 truncated tetrahedron
 truncated octahedron
 truncated cube
 truncated icosahedron
 truncated dodecahedron
Birectification (2r)
Dual (d)		2r{p,q}
 tetrahedron
 octahedron
 cube
 icosahedron
 dodecahedron
cantellation (rr)
Expansion (e)		rr{p,q}
 rhombitetratetrahedron
 rhombicuboctahedron
rhombicosidodecahedron
Snub rectified (sr)
Snub (s)		sr{p,q}
 snub tetratetrahedron
 snub cuboctahedron
 snub icosidodecahedron
Cantitruncation (tr)
Bevel (b)		tr{p,q}
 truncated tetratetrahedron
 truncated cuboctahedron
 truncated icosidodecahedron

Note the duality between the cube and the octahedron, and between the dodecahedron and the icosahedron. Also, in part due to self-duality of the tetrahedron, only one Archimedean solid has only tetrahedral symmetry.

See also

Notes

  1. 1 2 Grünbaum (2009).
  2. ↑ Field J., Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler, Archive for History of Exact Sciences, 50, 1997, 227
  3. ↑ Malkevitch (1988), p. 85

References

External links

This article is issued from Wikipedia - version of the Tuesday, February 09, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.