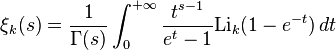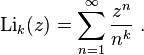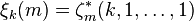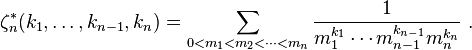Arakawa–Kaneko zeta function

In mathematics, the Arakawa–Kaneko zeta function is a generalisation of the Riemann zeta function which generates special values of the polylogarithm function.

Definition

The zeta function 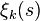$\xi_k(s)$ is defined by

\xi_k(s) = \frac{1}{\Gamma(s)} \int_0^{+\infty} \frac{t^{s-1}}{e^t-1}\mathrm{Li}_k(1-e^{-t}) \, dt \

where Li_k is the k-th polylogarithm

\mathrm{Li}_k(z) = \sum_{n=1}^{\infty} \frac{z^n}{n^k} \ .

Properties

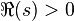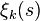The integral converges for $\Re(s) > 0$ and $\xi_k(s)$ has analytic continuation to the whole complex plane as an entire function.

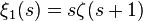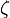The special case k = 1 gives $\xi_1(s) = s \zeta(s+1)$ where $\zeta$ is the Riemann zeta-function.

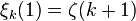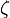The special case s = 1 remarkably also gives $\xi_k(1) = \zeta(k+1)$ where $\zeta$ is the Riemann zeta-function.

The values at integers are related to multiple zeta function values by

\xi_k(m) = \zeta_m^*(k,1,\ldots,1)

where

\zeta_n^*(k_1,\dots,k_{n-1},k_n)=\sum_{0<m_1<m_2<\cdots<m_n}\frac{1}{m_1^{k_1}\cdots m_{n-1}^{k_{n-1}}m_n^{k_n}} \ .

References

Kaneko, Masanobou (1997). "Poly-Bernoulli numbers". J. Théor. Nombres Bordx. 9: 221–228. Zbl 0887.11011.
Arakawa, Tsuneo; Kaneko, Masanobu (1999). "Multiple zeta values, poly-Bernoulli numbers, and related zeta functions". Nagoya Math. J. 153: 189–209. MR 1684557. Zbl 0932.11055.
Coppo, Marc-Antoine; Candelpergher, Bernard (2010). "The Arakawa–Kaneko zeta function". Ramanujan J. 22: 153–162. Zbl 1230.11106.

This article is issued from Wikipedia - version of the Friday, May 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.