Apriori algorithm

Apriori^[1] is an algorithm for frequent item set mining and association rule learning over transactional databases. It proceeds by identifying the frequent individual items in the database and extending them to larger and larger item sets as long as those item sets appear sufficiently often in the database. The frequent item sets determined by Apriori can be used to determine association rules which highlight general trends in the database: this has applications in domains such as market basket analysis.

Overview

The Apriori algorithm was proposed by Agarwal and Srikant in 1994. Apriori is designed to operate on databases containing transactions (for example, collections of items bought by customers, or details of a website frequentation). Other algorithms are designed for finding association rules in data having no transactions (Winepi and Minepi), or having no timestamps (DNA sequencing). Each transaction is seen as a set of items (an itemset). Given a threshold 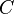$C$ , the Apriori algorithm identifies the item sets which are subsets of at least 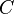$C$ transactions in the database.

Apriori uses a "bottom up" approach, where frequent subsets are extended one item at a time (a step known as candidate generation), and groups of candidates are tested against the data. The algorithm terminates when no further successful extensions are found.

Apriori uses breadth-first search and a Hash tree structure to count candidate item sets efficiently. It generates candidate item sets of length $k$ from item sets of length $k-1$ . Then it prunes the candidates which have an infrequent sub pattern. According to the downward closure lemma, the candidate set contains all frequent $k$ -length item sets. After that, it scans the transaction database to determine frequent item sets among the candidates.

The pseudo code for the algorithm is given below for a transaction database $T$ , and a support threshold of $\epsilon$ . Usual set theoretic notation is employed, though note that $T$ is a multiset. $C_k$ is the candidate set for level $k$ . At each step, the algorithm is assumed to generate the candidate sets from the large item sets of the preceding level, heeding the downward closure lemma. $count[c]$ accesses a field of the data structure that represents candidate set $c$ , which is initially assumed to be zero. Many details are omitted below, usually the most important part of the implementation is the data structure used for storing the candidate sets, and counting their frequencies.

$\begin{align} & \mathrm{Apriori}(T,\epsilon)\\ &\qquad L_1 \gets \{ \mathrm{large~1-item sets} \} \\ &\qquad k \gets 2\\ &\qquad \mathrm{\textbf{while}}~ L_{k-1} \neq \ \emptyset \\ &\qquad \qquad C_k \gets \{ a \cup \{b\} \mid a \in L_{k-1} \land b \not \in a \} - \{ c \mid \{ s \mid s \subseteq c \land |s| = k-1 \} \nsubseteq L_{k-1} \}\\ &\qquad \qquad \mathrm{\textbf{for}~transactions}~t \in T\\ &\qquad \qquad\qquad C_t \gets \{ c \mid c \in C_k \land c \subseteq t \} \\ &\qquad \qquad\qquad \mathrm{\textbf{for}~candidates}~c \in C_t\\ &\qquad \qquad\qquad\qquad \mathit{count}[c] \gets \mathit{count}[c]+1\\ &\qquad \qquad L_k \gets \{ c \mid c \in C_k \land ~ \mathit{count}[c] \geq \epsilon \}\\ &\qquad \qquad k \gets k+1\\ &\qquad \mathrm{\textbf{return}}~\bigcup_k L_k \end{align}$

Examples

Example 1

Consider the following database, where each row is a transaction and each cell is an individual item of the transaction:

alpha	beta	epsilon
alpha	beta	theta
alpha	beta	epsilon
alpha	beta	theta

The association rules that can be determined from this database are the following:

100% of sets with alpha also contain beta
50% of sets with alpha, beta also have epsilon
50% of sets with alpha, beta also have theta

we can also illustrate this through a variety of examples

Example 2

Assume that a large supermarket tracks sales data by stock-keeping unit (SKU) for each item: each item, such as "butter" or "bread", is identified by a numerical SKU. The supermarket has a database of transactions where each transaction is a set of SKUs that were bought together.

Let the database of transactions consist of following itemsets:

Itemsets
{1,2,3,4}
{1,2,4}
{1,2}
{2,3,4}
{2,3}
{3,4}
{2,4}

We will use Apriori to determine the frequent item sets of this database. To do so, we will say that an item set is frequent if it appears in at least 3 transactions of the database: the value 3 is the support threshold.

The first step of Apriori is to count up the number of occurrences, called the support, of each member item separately, by scanning the database a first time. We obtain the following result

Item	Support
{1}	3
{2}	6
{3}	4
{4}	5

All the itemsets of size 1 have a support of at least 3, so they are all frequent.

The next step is to generate a list of all pairs of the frequent items:

Item	Support
{1,2}	3
{1,3}	1
{1,4}	2
{2,3}	3
{2,4}	4
{3,4}	3

The pairs {1,2}, {2,3}, {2,4}, and {3,4} all meet or exceed the minimum support of 3, so they are frequent. The pairs {1,3} and {1,4} are not. Now, because {1,3} and {1,4} are not frequent, any larger set which contains {1,3} or {1,4} cannot be frequent. In this way, we can prune sets: we will now look for frequent triples in the database, but we can already exclude all the triples that contain one of these two pairs:

Item	Support
{2,3,4}	2

in the example, there are no frequent triplets -- {2,3,4} is below the minimal threshold, and the other triplets were excluded because they were super sets of pairs that were already below the threshold.

We have thus determined the frequent sets of items in the database, and illustrated how some items were not counted because one of their subsets was already known to be below the threshold.

Limitations

Apriori, while historically significant, suffers from a number of inefficiencies or trade-offs, which have spawned other algorithms. Candidate generation generates large numbers of subsets (the algorithm attempts to load up the candidate set with as many as possible before each scan). Bottom-up subset exploration (essentially a breadth-first traversal of the subset lattice) finds any maximal subset S only after all 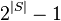$2^{|S|}-1$ of its proper subsets.

Later algorithms such as Max-Miner^[2] try to identify the maximal frequent item sets without enumerating their subsets, and perform "jumps" in the search space rather than a purely bottom-up approach.

References

↑ Rakesh Agrawal and Ramakrishnan Srikant Fast algorithms for mining association rules in large databases. Proceedings of the 20th International Conference on Very Large Data Bases, VLDB, pages 487-499, Santiago, Chile, September 1994.
↑ Bayardo Jr, Roberto J. (1998). "Efficiently mining long patterns from databases" (PDF). ACM Sigmod Record. 27 (2).

External links

ARtool, GPL Java association rule mining application with GUI, offering implementations of multiple algorithms for discovery of frequent patterns and extraction of association rules (includes Apriori)
ELKI includes Java implementations of Apriori, Eclat and FPGrowth.
SPMF offers Java open-source implementations of Apriori and several variations such as AprioriClose, UApriori, AprioriInverse, AprioriRare, MSApriori, AprioriTID, and other more efficient algorithms such as FPGrowth and LCM.
Christian Borgelt provides C implementations for Apriori and many other frequent pattern mining algorithms (Eclat, FPGrowth, etc.). The code is distributed as free software under the MIT license.
The R package arules contains Apriori and Eclat and infrastructure for representing, manipulating and analyzing transaction data and patterns.
Orange, an open-source data mining suite, contains widgets for enumerating itemsets and association rules based on Apriori algorithm.

This article is issued from Wikipedia - version of the Monday, December 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.