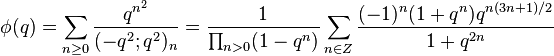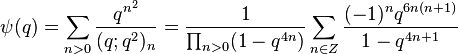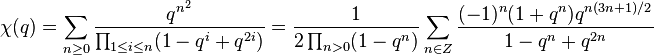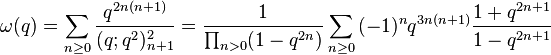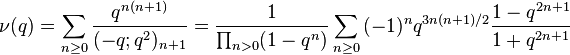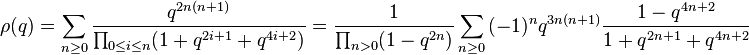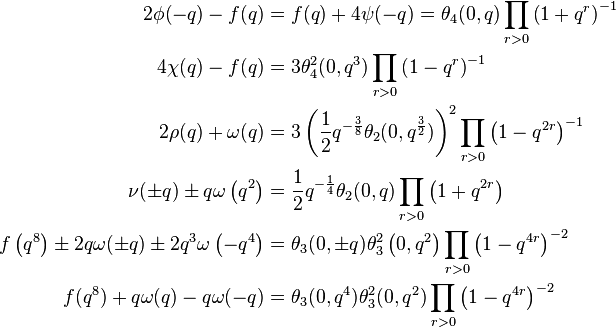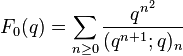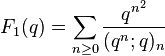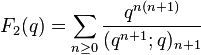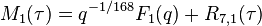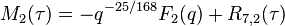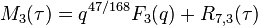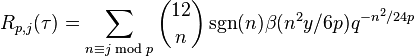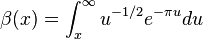Mock modular form
In mathematics, a mock modular form is the holomorphic part of a harmonic weak Maass form, and a mock theta function is essentially a mock modular form of weight 1/2. The first examples of mock theta functions were described by Srinivasa Ramanujan in his last 1920 letter to G. H. Hardy and in his lost notebook. Sander Zwegers (2001, 2002) discovered that adding certain non-holomorphic functions to them turns them into harmonic weak Maass forms.
History
"Suppose there is a function in the Eulerian form and suppose that all or an infinity of points are exponential singularities, and also suppose that at these points the asymptotic form closes as neatly as in the cases of (A) and (B). The question is: Is the function taken the sum of two functions one of which is an ordinary θ-function and the other a (trivial) function which is O(1) at all the points e2mπi/n? ... When it is not so, I call the function a Mock θ-function."
Ramanujan's 12 January 1920 letter to Hardy, reprinted in (Ramanujan 2000, Appendix II), listed 17 examples of functions that he called mock theta functions, and his lost notebook (Ramanujan 1988) contained several more examples. (Ramanujan used the term "theta function" for what today would be called a modular form.) Ramanujan pointed out that they have an asymptotic expansion at the cusps, similar to that of modular forms of weight 1/2, possibly with poles at cusps, but cannot be expressed in terms of "ordinary" theta functions. He called functions with similar properties "mock theta functions". Zwegers later discovered the connection of the mock theta function with weak Maass forms.
Ramanujan associated an order to his mock theta functions, which was not clearly defined. Before the work of Zwegers, the orders of known mock theta functions included
- 3, 5, 6, 7, 8, 10.
Ramanujan's notion of order later turned out to correspond to the conductor of the Nebentypus character of the weight 1⁄2 harmonic Maass forms which admit Ramanujan's mock theta functions as their holomorphic projections.
In the next few decades, Ramanujan's mock theta functions were studied by Watson, Andrews, Selberg, Hickerson, Choi, McIntosh, and others, who proved Ramanujan's statements about them and found several more examples and identities. (Most of the "new" identities and examples were already known to Ramanujan and reappeared in his lost notebook.) Watson (1936) found that under the action of elements of the modular group, the order 3 mock theta functions almost transform like modular forms of weight 1/2 (multiplied by suitable powers of q), except that there are "error terms" in the functional equations, usually given as explicit integrals. However for many years there was no good definition of a mock theta function. This changed in 2001 when Zwegers discovered the relation with non-holomorphic modular forms, Lerch sums, and indefinite theta series. Zwegers (2002) showed, using the previous work of Watson and Andrews, that the mock theta functions of orders 3, 5, and 7 can be written as the sum of a weak Maass form of weight 1⁄2 and a function that is bounded along geodesics ending at cusps. The weak Maass form has eigenvalue 3/16 under the hyperbolic Laplacian (the same value as holomorphic modular forms of weight 1⁄2); however, it increases exponentially fast near cusps, so it does not satisfy the usual growth condition for Maass wave forms. Zwegers proved this result in three different ways, by relating the mock theta functions to Hecke's theta functions of indefinite lattices of dimension 2, and to Appell–Lerch sums, and to meromorphic Jacobi forms.
Zwegers's fundamental result shows that mock theta functions are the "holomorphic parts" of real analytic modular forms of weight 1/2. This allows one to extend many results about modular forms to mock theta functions. In particular, like modular forms, mock theta functions all lie in certain explicit finite-dimensional spaces, which reduces the long and hard proofs of many identities between them to routine linear algebra. For the first time it became possible to produce infinite numbers of examples of mock theta functions; before this work there were only about 50 examples known (most of which were first found by Ramanujan). As further applications of Zwegers's ideas, Kathrin Bringmann and Ken Ono showed that certain q-series arising from the Rogers–Fine basic hypergeometric series are related to holomorphic parts of weight 3/2 harmonic weak Maass forms (Bringmann, Folsom & Ono 2009) and showed that the asymptotic series for coefficients of the order 3 mock theta function f(q) studied by (Andrews 1966) and Dragonette (1952) converges to the coefficients (Bringmann & Ono 2006). In particular Mock theta functions have asymptotic expansions at cusps of the modular group, acting on the upper half-plane, that resemble those of modular forms of weight 1/2 with poles at the cusps.
Definition
A mock modular form will be defined as the "holomorphic part" of a harmonic weak Maass form.
Fix a weight k, usually with 2k integral. Fix a subgroup Γ of SL2(Z) (or of the metaplectic group if k is half-integral) and a character ρ of Γ. A modular form f for this character and this group Γ transforms under elements of Γ by
A weak Maass form of weight k is a continuous function on the upper half plane that transforms like a modular form of weight 2 − k and is an eigenfunction of the weight k Laplacian operator, and is called harmonic if its eigenvalue is (1 − k/2)k/2 (Bruinier & Funke 2004). This is the eigenvalue of holomorphic weight k modular forms, so these are all examples of harmonic weak Maass forms. (A Maass form is a weak Maass form that decreases rapidly at cusps.) So a harmonic weak Maass form is annihilated by the differential operator
If F is any harmonic weak Maass form then the function g given by
is holomorphic and transforms like a modular form of weight k, though it may not be holomorphic at cusps. If we can find any other function g* with the same image g, then F − g* will be holomorphic. Such a function is given by inverting the differential operator by integration; for example we can define
where
is essentially the incomplete gamma function. The integral converges whenever g has a zero at the cusp i∞, and the incomplete gamma function can be extended by analytic continuation, so this formula can be used to define the holomorphic part g* of F even in the case when g is meromorphic at i∞, though this requires some care if k is 1 or not integral or if n = 0. The inverse of the differential operator is far from unique as we can add any homomorphic function to g* without affecting its image, and as a result the function g* need not be invariant under the group Γ. The function h = F − g* is called the holomorphic part of F.
A mock modular form is defined to be the holomorphic part h of some harmonic weak Maass form F. So there is an isomorphism from the space of mock modular forms h to a subspace of the harmonic weak Maass forms.
The mock modular form h is holomorphic but not quite modular, while h + g* is modular but not quite holomorphic. The space of mock modular forms of weight k contains the space of nearly modular forms ("modular forms that may be meromorphic at cusps") of weight k as a subspace. The quotient is (antilinearly) isomorphic to the space of holomorphic modular forms of weight 2 − k. The weight-(2 − k) modular form g corresponding to a mock modular form h is called its shadow. It is quite common for different mock theta functions to have the same shadow. For example, the 10 mock theta functions of order 5 found by Ramanujan fall into two groups of 5, where all the functions in each group have the same shadow (up to multiplication by a constant).
Zagier (2007) defines a mock theta function as a rational power of q = e2πiτ times a mock modular form of weight 1/2 whose shadow is a theta series of the form
for a positive rational κ and an odd periodic function ε. (Any such theta series is a modular form of weight 3/2). The rational power of q is a historical accident.
Most mock modular forms and weak Maass forms have rapid growth at cusps. It is common to impose the condition that they grow at most exponentially fast at cusps (which for mock modular forms means they are "meromorphic" at cusps). The space of mock modular forms (of given weight and group) whose growth is bounded by some fixed exponential function at cusps is finite-dimensional.
Appell–Lerch sums
Appell–Lerch sums were first studied by Paul Émile Appell (1884) and Mathias Lerch (1892). Watson studied the order 3 mock theta functions by expressing them in terms of Appell–Lerch sums, and Zwegers used them to show that mock theta functions are essentially mock modular forms.
The Appell–Lerch series is
where
and
The modified series
where
and y = Im(τ) and
satisfies the following transformation properties
In other words the modified Appell–Lerch series transforms like a modular form with respect to τ. Since mock theta functions can be expressed in terms of Appell–Lerch series this means that mock theta functions transform like modular forms if they have a certain non-analytic series added to them.
Indefinite theta series
Andrews (1986) showed that several of Ramanujan’s fifth order mock theta functions are equal to quotients Θ(τ)/θ(τ) where θ(τ) is a modular form of weight 1/2 and Θ(τ) is a theta function of an indefinite binary quadratic form, and Hickerson (1988b) proved similar results for seventh order mock theta functions. Zwegers showed how to complete the indefinite theta functions to produce real analytic modular forms, and used this to give another proof of the relation between mock theta functions and weak Maass wave forms.
Meromorphic Jacobi forms
Andrews (1988) observed that some of Ramanujan's fifth order mock theta functions could be expressed in terms of quotients of Jacobi's theta functions. Zwegers used this idea to express mock theta functions as Fourier coefficients of meromorphic Jacobi forms.
Applications
- Lawrence & Zagier (1999) related mock theta functions to quantum invariants of 3-manifolds.
- Semikhatov, Taormina & Tipunin (2005) related mock theta functions to infinite-dimensional Lie superalgebras and conformal field theory.
- Troost (2010) showed that the modular completions of mock modular forms arise as elliptic genera of conformal field theories with continuous spectrum.
- Mock theta functions appear in the theory of umbral moonshine.
- Atish Dabholkar, Sameer Murthy, and Don Zagier (2012) showed that mock modular forms are related to the numbers of BPS states in N=4 string theories.
Examples
- Any modular form of weight k (possibly only meromorphic at cusps) is a mock modular form of weight k with shadow 0.
- The quasimodular Eisenstein series
- of weight 2 and level 1 is a mock modular form of weight 2, with shadow a constant. This means that
- transforms like a modular form of weight 2 (where τ = x + iy).
- The function studied by Zagier (1975) (Hirzebruch & Zagier 1976, 2.2) with Fourier coefficients that are Hurwitz class numbers H(N) of imaginary quadratic fields is a mock modular form of weight 3/2, level 4 and shadow ∑ q n2. The corresponding weak Maass wave form is
- where
- and y = Im(τ), q = e2πiτ.
Mock theta functions are mock modular forms of weight 1/2 whose shadow is a unary theta function, multiplied by a rational power of q (for historical reasons). Before the work of Zwegers led to a general method for constructing them, most examples were given as basic hypergeometric functions, but this is largely a historical accident, and most mock theta functions have no known simple expression in terms of such functions.
The "trivial" mock theta functions are the (holomorphic) modular forms of weight 1/2, which were classified by Serre & Stark (1977), who showed that they could all be written in terms of theta functions of 1-dimensional lattices.
The following examples use the q-Pochhammer symbols  which are defined as:
which are defined as:
Order 2
Some order 2 mock theta functions were studied by (McIntosh 2007).
The function μ was found by Ramanujan in his lost notebook.
These are related to the functions listed in the section on order 8 functions by
Order 3
Ramanujan mentioned four order-3 mock theta functions in his letter to Hardy, and listed a further three in his lost notebook, which were rediscovered by G. N. Watson. Watson (1936) proved the relations between them stated by Ramanujan and also found their transformations under elements of the modular group by expressing them as Appell–Lerch sums. Dragonette (1952) described the asymptotic expansion of their coefficients. Zwegers (2000) related them to harmonic weak Maass forms. See also (Fine 1988)
The seven order-3 mock theta functions given by Ramanujan are
The first four of these form a group with the same shadow (up to a constant), and so do the last three. More precisely, the functions satisfy the following relations (found by Ramanujan and proved by Watson):
Order 5
Ramanujan wrote down ten mock theta functions of order 5 in his 1920 letter to Hardy, and stated some relations between them that were proved by Watson (1937). In his lost notebook he stated some further identities relating these functions, equivalent to the mock theta conjectures (Andrews & Garvan 1989), that were proved by Hickerson (1988). Andrews (1986) found representations of many of these functions as the quotient of an indefinite theta series by modular forms of weight 1/2.
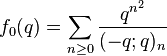 (sequence A053256 in OEIS)
(sequence A053256 in OEIS)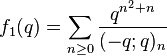 (sequence A053257 in OEIS)
(sequence A053257 in OEIS)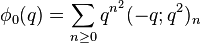 (sequence A053258 in OEIS)
(sequence A053258 in OEIS)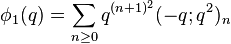 (sequence A053259 in OEIS)
(sequence A053259 in OEIS)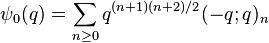 (sequence A053260 in OEIS)
(sequence A053260 in OEIS)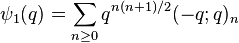 (sequence A053261 in OEIS)
(sequence A053261 in OEIS)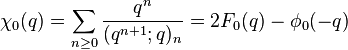 (sequence A053262 in OEIS)
(sequence A053262 in OEIS)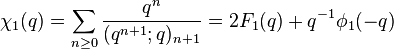 (sequence A053263 in OEIS)
(sequence A053263 in OEIS)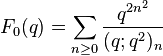 (sequence A053264 in OEIS)
(sequence A053264 in OEIS)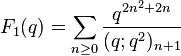 (sequence A053265 in OEIS)
(sequence A053265 in OEIS)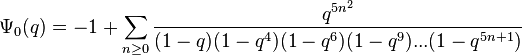 (sequence A053266 in OEIS)
(sequence A053266 in OEIS)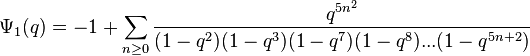 (sequence A053267 in OEIS)
(sequence A053267 in OEIS)
Order 6
Ramanujan (1988) wrote down seven mock theta functions of order 6 in his lost notebook, and stated 11 identities between them, which were proved in (Andrews & Hickerson 1991). Two of Ramanujan's identities relate φ and ψ at various arguments, four of them express φ and ψ in terms of Appell–Lerch series, and the last five identities express the remaining five sixth-order mock theta functions in terms of φ and ψ. Berndt & Chan (2007) discovered two more sixth order functions. The order 6 mock theta functions are:
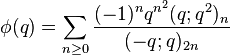 (sequence A053268 in OEIS)
(sequence A053268 in OEIS)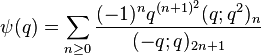 (sequence A053269 in OEIS)
(sequence A053269 in OEIS)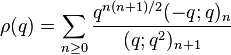 (sequence A053270 in OEIS)
(sequence A053270 in OEIS)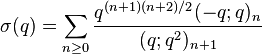 (sequence A053271 in OEIS)
(sequence A053271 in OEIS)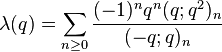 (sequence A053272 in OEIS)
(sequence A053272 in OEIS)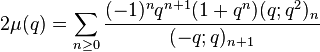 (sequence A053273 in OEIS)
(sequence A053273 in OEIS)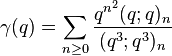 (sequence A053274 in OEIS)
(sequence A053274 in OEIS)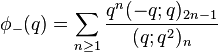 (sequence A153251 in OEIS)
(sequence A153251 in OEIS)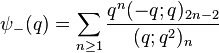 (sequence A153252 in OEIS)
(sequence A153252 in OEIS)
Order 7
Ramanujan gave three mock theta functions of order 7 in his 1920 letter to Hardy. They were studied by Selberg (1938), who found asymptotic expansion for their coefficients, and in (Andrews 1986). Hickerson (1988) found representations of many of these functions as the quotients of indefinite theta series by modular forms of weight 1/2. Zwegers (2001, 2002) described their modular transformation properties.
These three mock theta functions have different shadows, so unlike the case of Ramanujan's order 3 and order 5 functions, there are no linear relations between them and ordinary modular forms. The corresponding weak Maass forms are
where
and
is more or less the complementary error function. Under the metaplectic group, these three functions transform according to a certain 3-dimensional representation of the metaplectic group as follows
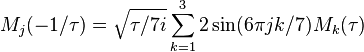
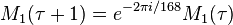 ,
, 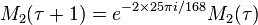 ,
, 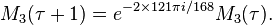
In other words, they are the components of a level 1 vector-valued harmonic weak Maass form of weight 1/2.
Order 8
Gordon & McIntosh (2000) found eight mock theta functions of order 8. They found five linear relations involving them, and expressed four of the functions as Appell–Lerch sums, and described their transformations under the modular group. The two functions V1 and U0 were found earlier by Ramanujan (1988, p. 8, eqn 1; p. 29 eqn 6) in his lost notebook.
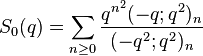 (sequence A153148 in OEIS)
(sequence A153148 in OEIS)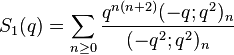 (sequence A153149 in OEIS)
(sequence A153149 in OEIS)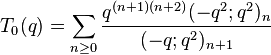 (sequence A153155 in OEIS)
(sequence A153155 in OEIS)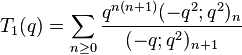 (sequence A153156 in OEIS)
(sequence A153156 in OEIS)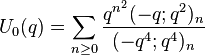 (sequence A153172 in OEIS)
(sequence A153172 in OEIS)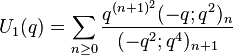 (sequence A153174 in OEIS)
(sequence A153174 in OEIS)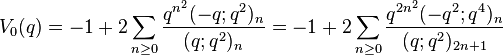 (sequence A153176 in OEIS)
(sequence A153176 in OEIS)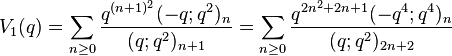 (sequence A153178 in OEIS)
(sequence A153178 in OEIS)
Order 10
Ramanujan (1988, p. 9) listed four order-10 mock theta functions in his lost notebook, and stated some relations between them, which were proved by Choi (1999, 2000, 2002, 2007).
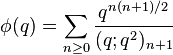 (sequence A053281 in OEIS)
(sequence A053281 in OEIS)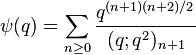 (sequence A053282 in OEIS)
(sequence A053282 in OEIS)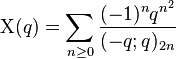 (sequence A053283 in OEIS)
(sequence A053283 in OEIS)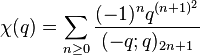 (sequence A053284 in OEIS)
(sequence A053284 in OEIS)
References
- Andrews, George E. (1966), "On the theorems of Watson and Dragonette for Ramanujan's mock theta functions", American Journal of Mathematics 88 (2): 454–490, doi:10.2307/2373202, ISSN 0002-9327, JSTOR 2373202, MR 0200258
- Andrews, George E. (1986), "The fifth and seventh order mock theta functions", Transactions of the American Mathematical Society 293 (1): 113–134, doi:10.2307/2000275, ISSN 0002-9947, JSTOR 2000275, MR 814916
- Andrews, George E. (1989), "Theta functions—Bowdoin 1987, Part 2 (Brunswick, ME, 1987)", American Mathematical Society, Proc. Sympos. Pure Math. (Providence, R.I.) 49: 283–298, MR 1013178
|chapter=ignored (help) - Andrews, George E. (1988), "Ramanujan's fifth order mock theta functions as constant terms", Ramanujan revisited (Urbana-Champaign, Ill., 1987), Boston, MA: Academic Press, pp. 47–56, MR 938959
- Andrews, George E.; Garvan, F. G. (1989), "Ramanujan's lost notebook. VI. The mock theta conjectures", Advances in Mathematics 73 (2): 242–255, doi:10.1016/0001-8708(89)90070-4, ISSN 0001-8708, MR 987276
- Andrews, George E.; Hickerson, Dean (1991), "Ramanujan's lost notebook. VII. The sixth order mock theta functions", Advances in Mathematics 89 (1): 60–105, doi:10.1016/0001-8708(91)90083-J, ISSN 0001-8708, MR 1123099
- Appell, P. (1884), "Sur les fonctions doublement périodiques de troisième espèce", Annales Scientifiques de l'École Normale Supérieure 1: 135–164
- Berndt, Bruce C.; Chan, Song Heng (2007), "Sixth order mock theta functions", Advances in Mathematics 216 (2): 771–786, doi:10.1016/j.aim.2007.06.004, ISSN 0001-8708, MR 2351377
- Bringmann, Kathrin; Ono, Ken (2007), "Lifting cusp forms to Maass forms with an application to partitions" (PDF), Proceedings of the National Academy of Sciences of the United States of America 104 (10): 3725–3731, doi:10.1073/pnas.0611414104, ISSN 0027-8424, MR 2301875, PMC 1820651, PMID 17360420
- Bringmann, Kathrin; Ono, Ken (2006), "The f(q) mock theta function conjecture and partition ranks" (PDF), Inventiones Mathematicae 165 (2): 243–266, doi:10.1007/s00222-005-0493-5, ISSN 0020-9910, MR 2231957
- Bringmann, Kathrin; Ono, Ken, "Dyson's ranks and Maass forms" (PDF), Annals of Mathematics, doi:10.4007/annals.2010.171.419
- Bruinier, Jan Hendrik; Funke, Jens (2004), "On two geometric theta lifts", Duke Mathematical Journal 125 (1): 45–90, doi:10.1215/S0012-7094-04-12513-8, ISSN 0012-7094, MR 2097357
- Choi, Youn-Seo (1999), "Tenth order mock theta functions in Ramanujan's lost notebook", Inventiones Mathematicae 136 (3): 497–569, doi:10.1007/s002220050318, ISSN 0020-9910, MR 1695205
- Choi, Youn-Seo (2000), "Tenth order mock theta functions in Ramanujan's lost notebook. II", Advances in Mathematics 156 (2): 180–285, doi:10.1006/aima.2000.1948, ISSN 0001-8708, MR 1808245
- Choi, Youn-Seo (2002), "Tenth order mock theta functions in Ramanujan's lost notebook. IV", Transactions of the American Mathematical Society 354 (2): 705–733, doi:10.1090/S0002-9947-01-02861-6, ISSN 0002-9947, JSTOR 2693766, MR 1862564
- Choi, Youn-Seo (2007), "Tenth order mock theta functions in Ramanujan's lost notebook. III", Proceedings of the London Mathematical Society 94 (1): 26–52, doi:10.1112/plms/pdl006, ISSN 0024-6115, MR 2293464
- Dabholkar, Atish; Murthy, Sameer; Zagier, Don (2012), Quantum Black Holes, Wall Crossing, and Mock Modular Forms, arXiv:1208.4074
- Dragonette, Leila A. (1952), "Some asymptotic formulae for the mock theta series of Ramanujan", Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 72, No. 3) 72 (3): 474–500, doi:10.2307/1990714, ISSN 0002-9947, JSTOR 1990714, MR 0049927
- Fine, Nathan J. (1988), Basic hypergeometric series and applications, Mathematical Surveys and Monographs 27, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1524-3, MR 956465
- Garthwaite, Sharon Anne (2008), "The coefficients of the ω(q) mock theta function", International Journal of Number Theory 4 (6): 1027–1042, doi:10.1142/S1793042108001869, ISSN 1793-0421, MR 2483310
- Gordon, Basil; McIntosh, Richard J. (2000), "Some eighth order mock theta functions", Journal of the London Mathematical Society 62 (2): 321–335, doi:10.1112/S0024610700008735, ISSN 0024-6107, MR 1783627
- Hickerson, Dean (1988), "A proof of the mock theta conjectures", Inventiones Mathematicae 94 (3): 639–660, doi:10.1007/BF01394279, ISSN 0020-9910, MR 969247
- Hickerson, Dean (1988), "On the seventh order mock theta functions", Inventiones Mathematicae 94 (3): 661–677, doi:10.1007/BF01394280, ISSN 0020-9910, MR 969247
- Hirzebruch, Friedrich; Zagier, Don (1976), "Intersection numbers of curves on Hilbert modular surfaces and modular forms of Nebentypus", Inventiones Mathematicae 36: 57–113, doi:10.1007/BF01390005, ISSN 0020-9910, MR 0453649
- Lawrence, Ruth; Zagier, Don (1999), "Modular forms and quantum invariants of 3-manifolds", The Asian Journal of Mathematics 3 (1): 93–107, ISSN 1093-6106, MR 1701924
- Lerch, M. (1892), "Bemerkungen zur Theorie der elliptischen Funktionen", Jahrbuch uber die Fortschritte der Mathematik 24: 442–445
- McIntosh, Richard J. (2007), "Second order mock theta functions", Canadian Mathematical Bulletin 50 (2): 284–290, doi:10.4153/CMB-2007-028-9, ISSN 0008-4395, MR 2317449
- Ramanujan, Srinivasa (1988), The lost notebook and other unpublished papers, Berlin, New York: Springer-Verlag, ISBN 978-3-540-18726-4, MR 947735
- Ramanujan, Srinivasa (2000), Collected papers of Srinivasa Ramanujan, Providence, R.I.: AMS Chelsea Publishing, ISBN 978-0-8218-2076-6, MR 2280843
- Selberg, A. (1938), "Über die Mock-Thetafunktionen siebenter Ordnung. (On the mock theta functions of seventh order)", Archiv for Mathematik og Naturvidenskab 41: 3–15 Reprinted in volume I of his collected works.
- Semikhatov, A. M.; Taormina, A.; Tipunin, I. Yu. (2005), "Higher-level Appell functions, modular transformations, and characters", Communications in Mathematical Physics 255 (2): 469–512, doi:10.1007/s00220-004-1280-7, ISSN 0010-3616, MR 2129953
- Troost, J. (2010), "The Non-Compact Elliptic Genus : Mock or Modular", Journal of High Energy Physics 2010 (6), arXiv:1004.3649, doi:10.1007/JHEP06(2010)104
- Serre, Jean-Pierre; Stark, H. M. (1977), "Modular forms of weight 1/2", Modular functions of one variable, VI (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976), Lecture Notes in Mathematics 627, Berlin, New York: Springer-Verlag, pp. 27–67, doi:10.1007/BFb0065296, ISBN 978-3-540-08530-0, MR 0472707
- Watson, G. N. (1936), "The Final Problem : An Account of the Mock Theta Functions", Journal of the London Mathematical Society 11: 55–80, doi:10.1112/jlms/s1-11.1.55
- Watson, G. N. (1937), "The Mock Theta Functions (2)", Proceedings of the London Mathematical Society, s2-42: 274–304, doi:10.1112/plms/s2-42.1.274
- Zagier, Don (1975), "Nombres de classes et formes modulaires de poids 3/2", Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. Séries a et B 281 (21): Ai, A883–A886, ISSN 0151-0509, MR 0429750
- Zagier, Don (2009) [2007], "Séminaire Bourbaki. Vol. 2007/2008" (PDF), Astérisque, Séminaire Bourbaki Exp. 986 326: 143–164, ISBN 978-2-85629-269-3, ISSN 0303-1179, MR 2605321
|chapter=ignored (help) - Zwegers, S. P. (2002), Mock Theta Functions, Utrecht PhD thesis, ISBN 90-393-3155-3
- Zwegers, S. P. (2001), "Mock θ-functions and real analytic modular forms", q-series with applications to combinatorics, number theory, and physics (Urbana, IL, 2000) (PDF), Contemp. Math. 291, Providence, R.I.: American Mathematical Society, pp. 269–277, ISBN 978-0-8218-2746-8, MR 1874536
- Zwegers, S. P. (2008), Appell–Lerch sums as mock modular forms (PDF)
Further reading
- Ono, Ken (2008), "Mock theta functions, ranks and Maass forms", in Alladi, Krishnaswami, Surveys in Number Theory, Developments in Mathematics 17, Springer-Verlag, pp. 119–141, ISBN 978-0-387-78509-7, Zbl 1183.11064
External links
- International Conference: Mock theta functions and applications 2009
- Papers on mock theta functions by George Andrews
- Papers on mock theta functions by Kathrin Bringmann
- Papers on mock theta functions by Ken Ono
- Papers on mock theta functions by Sander Zwegers
- Weisstein, Eric W., "Mock Theta Function", MathWorld.
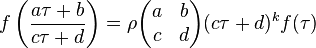
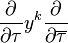
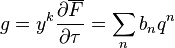
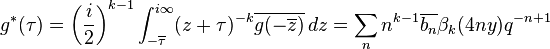
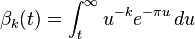
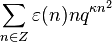
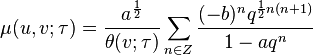
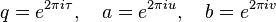
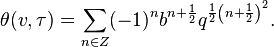
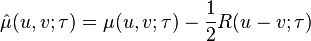
![R(z;\tau) = \sum_{\nu\in Z + \frac{1}{2}}(-1)^{\nu - \frac{1}{2}}\left({\rm sign}(\nu) - E\left[\left(\nu + \frac{\Im(z)}{y}\right)\sqrt{2y}\right]\right)e^{-2\pi i \nu z}q^{-\frac{1}{2}\nu^2}](../I/m/664a22180ce1688cfd0a25fc71f1c58b.png)
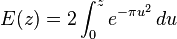
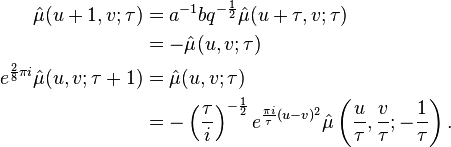
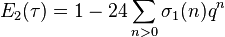
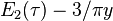
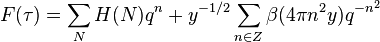
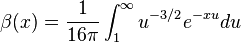
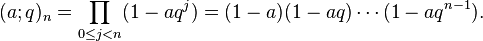
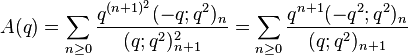
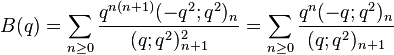
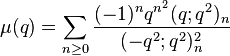
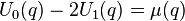
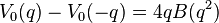
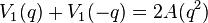
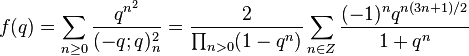 ,
,