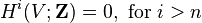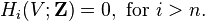Andreotti–Frankel theorem

In mathematics, the Andreotti–Frankel theorem, introduced by Andreotti and Frankel (1959), states that if $V$ is a smooth affine variety of complex dimension $n$ or, more generally, if $V$ is any Stein manifold of dimension $n$ , then in fact $V$ is homotopy equivalent to a CW complex of real dimension at most n. In other words $V$ has only half as much topology.

Consequently, if $V \subseteq \mathbb{C}^r$ is a closed connected complex submanifold of complex dimension $n$ , then $V$ has the homotopy type of a 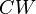$CW$ complex of real dimension $\le n$ . Therefore

H^i(V; \bold Z)=0,\text{ for }i>n \,

and

H_i(V; \bold Z)=0,\text{ for }i>n. \,

This theorem applies in particular to any smooth affine variety of dimension $n$ .

References

Andreotti, Aldo; Frankel, Theodore (1959), "The Lefschetz theorem on hyperplane sections", Annals of Mathematics. Second Series 69: 713–717, ISSN 0003-486X, JSTOR 1970034, MR 0177422
John Willard Milnor (1963), Morse Theory, Ch. 7.

This article is issued from Wikipedia - version of the Tuesday, July 14, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.