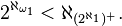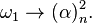András Hajnal

András Hajnal (born May 13, 1931) is an emeritus professor of mathematics at Rutgers University^[1] and a member of the Hungarian Academy of Sciences^[2] known for his work in set theory and combinatorics.

Biography

Hajnal was born on 13 May 1931,^[3] in Budapest, Hungary.

He received his university diploma (M.Sc. degree) in 1953 from the Eötvös Loránd University,^[4] his Candidate of Mathematical Science degree (roughly equivalent to Ph.D.) in 1957, under the supervision of László Kalmár,^[5] and his Doctor of Mathematical Science degree in 1962. From 1956 to 1995 he was a faculty member at the Eötvös Loránd University; in 1994, he moved to Rutgers University to become the director of DIMACS, and he remained there as a professor until his retirement in 2004.^[3] He became a member of the Hungarian Academy of Sciences in 1982, and directed its mathematical institute from 1982 to 1992.^[3] He was general secretary of the János Bolyai Mathematical Society from 1980 to 1990, and president of the society from 1990 to 1994.^[3] Since 1981, he has been an advisory editor of the journal Combinatorica.

In all his life, Hajnal has been an avid chess player.^[6]

Hajnal is the father of Peter Hajnal, the co-dean of the European College of Liberal Arts.

Research and publications

Hajnal is the author of over 150 publications.^[7] Among the many co-authors of Paul Erdős, he has the second largest number of joint papers, 56.^[8] With Peter Hamburger, he wrote a textbook, Set Theory (Cambridge University Press, 1999, ISBN 0-521-59667-X). Some of his more well-cited research papers^[9] include

A paper on circuit complexity with Maas, Pudlak, Szegedy, and György Turán,^[10] showing exponential lower bounds on the size of bounded-depth circuits with weighted majority gates that solve the problem of computing the parity of inner products.
The Hajnal–Szemerédi theorem on equitable coloring, proving a 1964 conjecture of Erdős:^[11] let Δ denote the maximum degree of a vertex in a finite graph G. Then G can be colored with Δ + 1 colors in such a way that the sizes of the color classes differ by at most one. Several authors have subsequently published simplifications and generalizations of this result.^[12]
A paper with Erdős and J. W. Moon on graphs that avoid having any k-cliques. Turán's theorem characterizes the graphs of this type with the maximum number of edges; Erdős, Hajnal and Moon find a similar characterization of the smallest maximal k-clique-free graphs, showing that they take the form of certain split graphs. This paper also proves a conjecture of Erdős and Gallai on the number of edges in a critical graph for domination.^[13]
A paper with Erdős on graph coloring problems for infinite graphs and hypergraphs.^[14] This paper extends greedy coloring methods from finite to infinite graphs: if the vertices of a graph can be well-ordered so that each vertex has few earlier neighbors, it has low chromatic number. When every finite subgraph has an ordering of this type in which the number of previous neighbors is at most k (that is, it is k-degenerate), an infinite graph has a well-ordering with at most 2k − 2 earlier neighbors per vertex. The paper also proves the nonexistence of infinite graphs with high finite girth and sufficiently large infinite chromatic number and the existence of graphs with high odd girth and infinite chromatic number.

Other selected results include:

In his dissertation^[15] he introduced the models L(A) (see relative constructibility), and proved that if κ is a regular cardinal and A is a subset of κ⁺, then ZFC and 2^κ = κ⁺ hold in L(A). This can be applied to prove relative consistency results: e.g., if 2^ℵ₀ = ℵ₂ is consistent then so is 2^ℵ₀ = ℵ₂ and 2^ℵ₁ = ℵ₂.
Hajnal's set mapping theorem, the solution to a conjecture of Stanisław Ruziewicz.^[16] This work concerns functions ƒ that map the members of an infinite set S to small subsets of S; more specifically, all subsets' cardinalities should be smaller than some upper bound that is itself smaller than the cardinality of S. Hajnal shows that S must have an equinumerous subset in which no pair of elements x and y have x in ƒ(y) or y in ƒ(x). This result greatly extends the case n = 1 of Kuratowski's free set theorem, which states that when ƒ maps an uncountable set to finite subsets there exists a pair x, y neither of which belongs to the image of the other.
An example of two graphs each with uncountable chromatic number, but with countably chromatic direct product.^[17] That is, Hedetniemi's conjecture fails for infinite graphs.
In a paper^[18] with Paul Erdős he proved several results on systems of infinite sets having property B.
A paper with Fred Galvin in which^[19] they proved that if 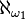$\aleph_{\omega_1}$ is a strong limit cardinal then
$2^{\aleph_{\omega_1}}<\aleph_{(2^{\aleph_1})^+}.$

This was the result which initiated Shelah's pcf theory.

With James Earl Baumgartner he proved a result in infinite Ramsey theory, that for every partition of the vertices of a complete graph on ω₁ vertices into finitely many subsets, at least one of the subsets contains a complete subgraph on α vertices, for every α < ω₁.^[20] This can be expressed using the notation of partition relations as
$\omega_1\to(\alpha)^2_n.$
With Matthew Foreman he proved that if κ is measurable then^[21] the partition relation 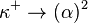$\kappa^+\to(\alpha)^2$ holds for α<Ω, where Ω<κ⁺ is a very large ordinal.
With István Juhász he published several results in set-theoretic topology. They first established^[22] the existence of Hausdorff spaces which are hereditarily separable, but not hereditarily Lindelöf, or vice versa. The existence of regular spaces with these properties (S-space and L-space) was much later settled, by Todorcevic and Moore.

Awards and honors

In 1992, Hajnal was awarded the Officer's Cross of the Order of the Republic of Hungary.^[3] In 1999, a conference in honor of his 70th birthday was held at DIMACS,^[23] and a second conference honoring the 70th birthdays of both Hajnal and Vera Sós was held in 2001 in Budapest.^[24] Hajnal became a fellow of the American Mathematical Society^[25] in 2012.

References

↑ Rutgers University Department of Mathematics – Emeritus Faculty.
↑ Hungarian Academy of Sciences, Section for Mathematics.
1 2 3 4 5 Curriculum vitae.
↑ A halmazelmélet huszadik századi "Hajnal A", M. Streho's interview with A. H., Magyar Tudomány, 2001.
↑ Andras Hajnal at the Mathematics Genealogy Project. The 1957 date is from Hajnal's cv; the mathematics genealogy site lists the date of Hajnal's Ph.D. as 1956.
↑ The announcement for the 2001 conference in honor of Hajnal and Sós calls him “the great chess player”; the conference included a blitz chess tournament in his honor.
↑ List of publications from Hajnal's web site.
↑ List of collaborators of Erdős by number of joint papers, from the Erdős number project web site.
↑ According to citation counts from Google scholar, retrieved March 1, 2009.
↑ Hajnal, A.; Maass, W.; Pudlak, P.; Szegedy, M.; Turán, G. (1987), "Threshold circuits of bounded depth", Proc. 28th Symp. Foundations of Computer Science (FOCS 1987), pp. 99–110, doi:10.1109/SFCS.1987.59 .
↑ Hajnal, A.; Szemerédi, E. (1970), "Proof of a conjecture of P. Erdős", Combinatorial theory and its applications, II (Proc. Colloq., Balatonfüred, 1969), North-Holland, pp. 601–623, MR 0297607 .
↑ Catlin, Paul A. (1980), "On the Hajnal–Szemerédi theorem on disjoint cliques", Utilitas Mathematica 17: 163–177, MR 583138 ; Fischer, Eldar (1999), "Variants of the Hajnal–Szemerédi theorem", Journal of Graph Theory 31 (4): 275–282, doi:10.1002/(SICI)1097-0118(199908)31:4<275::AID-JGT2>3.0.CO;2-F, MR 1698745 ; Kierstead, H. A.; Kostochka, A. V. (2008), "A short proof of the Hajnal–Szemerédi theorem on equitable colouring", Combinatorics, Probability and Computing 17 (2): 265–270, doi:10.1017/S0963548307008619, MR 2396352 ; Martin, Ryan; Szemerédi, Endre (2008), "Quadripartite version of the Hajnal–Szemerédi theorem", Discrete Mathematics 308 (19): 4337–4360, doi:10.1016/j.disc.2007.08.019, MR 2433861 .
↑ Erdős, P.; Hajnal, A.; Moon, J. W. (1964), "A problem in graph theory", American Mathematical Monthly (Mathematical Association of America) 71 (10): 1107–1110, doi:10.2307/2311408, JSTOR 2311408, MR 0170339 .
↑ Erdős, P.; Hajnal, A. (1966), "On chromatic number of graphs and set-systems", Acta Mathematica Hungarica 17 (1–2): 61–99, doi:10.1007/BF02020444, MR 0193025 .
↑ Hajnal, A. (1961), "On a consistency theorem connected with the generalized continuum problem", Acta Math. Acad. Sci. Hungar 12 (3–4): 321–376, doi:10.1007/BF02023921, MR 0150046 .
↑ Hajnal, A. (1961/1962), "Proof of a conjecture of S. Ruziewicz", Fund. Math. 50: 123–128, MR 0131986 Check date values in: |date= (help).
↑ Hajnal, A. (1985), "The chromatic number of the product of two ℵ₁ chromatic graphs can be countable", Combinatorica 5 (2): 137–140, doi:10.1007/BF02579376, MR 0815579. .
↑ P. Erdős, A. Hajnal: On a property of families of sets, Acta Math. Acad. Sci. Hungar., 12(1961), 87–123.
↑ Galvin, F.; Hajnal, A. (1975), "Inequalities for cardinal powers", Annals of Mathematics (2) 101 (3): 491–498, doi:10.2307/1970936, JSTOR 1970936 .
↑ Baumgartner, J.; Hajnal, A. (1973), "A proof (involving Martin's axiom) of a partition relation", Polska Akademia Nauk. Fundamenta Mathematicae 78 (3): 193–203, MR 0319768 . For additional results of Baumgartner and Hajnal on partition relations, see the following two papers: Baumgartner, J. E.; Hajnal, A. (1987), "A remark on partition relations for infinite ordinals with an application to finite combinatorics", Logic and combinatorics (Arcata, Calif., 1985), Contemp. Math. 65, Providence, RI: Amer. Math. Soc., pp. 157–167, MR 891246 ; Baumgartner, James E.; Hajnal, Andras (2001), "Polarized partition relations", The Journal of Symbolic Logic (Association for Symbolic Logic) 66 (2): 811–821, doi:10.2307/2695046, JSTOR 2695046, MR 1833480 .
↑ M. Foreman, A. Hajnal: A partition relation for successors of large cardinals, Math. Ann., 325(2003), 583–623.
↑ A. Hajnal, I. Juhász: On hereditarily α-Lindelöf and hereditarily α-separable spaces, Ann. Univ. Sci. Budapest. Eötvös Sect. Math., 11(1968), 115–124.
↑ Thomas, Simon, ed. (1999), Set Theory: The Hajnal Conference, October 15–17, 1999 DIMACS Center, DIMACS Series in Discrete Mathematics and Theoretical Computer Science 58, American Mathematical Society, ISBN 978-0-8218-2786-4 .
↑ Győri, Ervin; Katona, Gyula O. H.; Lovász, László, eds. (2006), More sets, graphs and numbers: a salute to Vera Sós and András Hajnal, Bolyai Society Mathematical Studies 15, Springer-Verlag, ISBN 978-3-540-32377-8 .
↑

External links

Authority control	WorldCat VIAF: 85621967 LCCN: n88624846 ISNI: 0000 0001 2142 2067 GND: 142654930 SUDOC: 070151660 BNF: cb12987483z (data) MGP: 24611 NKC: xx0050412

This article is issued from Wikipedia - version of the Tuesday, September 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.