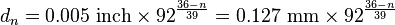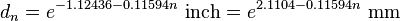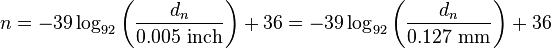American wire gauge

"AWG" redirects here. For other uses, see AWG (disambiguation).

American wire gauge (AWG), also known as the Brown & Sharpe wire gauge, is a standardized wire gauge system used since 1857 predominantly in North America for the diameters of round, solid, nonferrous, electrically conducting wire. Dimensions of the wires are given in ASTM standard B 258.^[1] The cross-sectional area of each gauge is an important factor for determining its current-carrying capacity.

Increasing gauge numbers denote decreasing wire diameters, which is similar to many other non-metric gauging systems such as SWG. This gauge system originated in the number of drawing operations used to produce a given gauge of wire. Very fine wire (for example, 30 gauge) required more passes through the drawing dies than 0 gauge wire did. Manufacturers of wire formerly had proprietary wire gauge systems; the development of standardized wire gauges rationalized selection of wire for a particular purpose.

The AWG tables are for a single, solid, round conductor. The AWG of a stranded wire is determined by the cross-sectional area of the equivalent solid conductor. Because there are also small gaps between the strands, a stranded wire will always have a slightly larger overall diameter than a solid wire with the same AWG.

AWG is also commonly used to specify body piercing jewelry sizes (especially smaller sizes), even when the material is not metallic.^[2]

Formula

By definition, No. 36 AWG is 0.005 inches in diameter, and No. 0000 is 0.46 inches in diameter. The ratio of these diameters is 1:92, and there are 40 gauge sizes from No. 36 to No. 0000, or 39 steps. Because each successive gauge number increases cross sectional area by a constant multiple, diameters vary geometrically. Any two successive gauges (e.g. A & B ) have diameters in the ratio (dia. B ÷ dia. A) of $\sqrt [39]{92}$ (approximately 1.12293), while for gauges two steps apart (e.g. A, B & C), the ratio of the C to A is about 1.12293² = 1.26098. The diameter of a No. n AWG wire is determined, for gauges smaller than 00 (36 to 0), according to the following formula:

d_n = 0.005~\mathrm{inch} \times 92 ^ \frac{36-n}{39} = 0.127~\mathrm{mm} \times 92 ^ \frac{36-n}{39}

(see below for gauges larger than No. 0 (i.e. No. 00, No. 000, No. 0000 ).) or equivalently

d_n = e^ {-1.12436 - 0.11594n}\ \mathrm{inch} = e^ {2.1104 - 0.11594n}\ \mathrm{mm}

The gauge can be calculated from the diameter using ^[3]

n = -39\log_{92} \left( \frac{d_{n}}{0.005~\mathrm{inch}} \right)+36 = -39\log_{92} \left( \frac{d_{n}}{0.127~\mathrm{mm}} \right)+36

and the cross-section area is

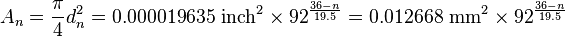A_n = \frac{\pi}{4} d_n^2 = 0.000019635~\mathrm{inch}^2 \times 92 ^ \frac{36-n}{19.5} = 0.012668~\mathrm{mm}^2 \times 92 ^ \frac{36-n}{19.5}

The standard ASTM B258 - 02(2008) Standard Specification for Standard Nominal Diameters and Cross-Sectional Areas of AWG Sizes of Solid Round Wires Used as Electrical Conductors defines the ratio between successive sizes to be the 39th root of 92, or approximately 1.1229322.^[4] ASTM B 258-02 also dictates that wire diameters should be tabulated with no more than 4 significant figures, with a resolution of no more than 0.0001 inches (0.1 mils) for wires larger than No. 44 AWG, and 0.00001 inches (0.01 mils) for wires No. 45 AWG and smaller.

Sizes with multiple zeros are successively larger than No. 0 and can be denoted using "number of zeros/0", for example 4/0 for 0000. For an m/0 AWG wire, use n = −(m−1) = 1−m in the above formulas. For instance, for No. 0000 or 4/0, use n = −3.

Rules of thumb

The sixth power of $\sqrt [39]{92}$ is very close to 2,^[5] which leads to the following rules of thumb:

When the diameter of a wire is doubled, the AWG will decrease by 6. (e.g., No. 2 AWG is about twice the diameter of No. 8 AWG.)
When the cross-sectional area of a wire is doubled, the AWG will decrease by 3. (e.g., Two No. 14 AWG wires have about the same cross-sectional area as a single No. 11 AWG wire.)
A decrease of ten gauge numbers, for example from No. 10 to 1/0, multiplies the area and weight by approximately 10 and reduces the resistance by a factor of approximately 10.
For the same cross section aluminum wire has a conductivity of approximately 61% of copper, so an aluminum wire has nearly the same resistance as a copper wire 2 AWG sizes smaller, which has 62.9% of the area.

Tables of AWG wire sizes

The table below shows various data including both the resistance of the various wire gauges and the allowable current (ampacity) based on plastic insulation. The diameter information in the table applies to solid wires. Stranded wires are calculated by calculating the equivalent cross sectional copper area. Fusing current (melting wire) is estimated based on 25°C ambient temperature. The table below assumes DC, or AC frequencies equal to or less than 60 Hz, and does not take skin effect into account. Turns of wire is an upper limit for wire with no insulation.

AWG	Diameter		Turns of wire, no insulation		Area		Copper resistance^[6]		NEC copper wire ampacity with 60/75/90 °C insulation (A)^[7]	Approx. stranded metric equivalents^[8]	Fusing current, copper^[9]^[10]
	(in)	(mm)	(per in)	(per cm)	(kcmil)	(mm²)	(Ω/km) (mΩ/m)	(Ω/kft) (mΩ/ft)			Preece, ~10 s	Onderdonk,
	(in)	(mm)	(per in)	(per cm)	(kcmil)	(mm²)	(Ω/km) (mΩ/m)	(Ω/kft) (mΩ/ft)			Preece, ~10 s	1 s	32 ms
0000 (4/0)	0.4600*	11.684*	2.17	0.856	212	107	0.1608	0.04901	195 / 230 / 260		3.2 kA	33 kA	182 kA
000 (3/0)	0.4096	10.405	2.44	0.961	168	85.0	0.2028	0.06180	165 / 200 / 225		2.7 kA	26 kA	144 kA
00 (2/0)	0.3648	9.266	2.74	1.08	133	67.4	0.2557	0.07793	145 / 175 / 195		2.3 kA	21 kA	115 kA
0 (1/0)	0.3249	8.251	3.08	1.21	106	53.5	0.3224	0.09827	125 / 150 / 170		1.9 kA	16 kA	91 kA
1	0.2893	7.348	3.46	1.36	83.7	42.4	0.4066	0.1239	110 / 130 / 145		1.6 kA	13 kA	72 kA
2	0.2576	6.544	3.88	1.53	66.4	33.6	0.5127	0.1563	95 / 115 / 130		1.3 kA	10.2 kA	57 kA
3	0.2294	5.827	4.36	1.72	52.6	26.7	0.6465	0.1970	85 / 100 / 115	196/0.4	1.1 kA	8.1 kA	45 kA
4	0.2043	5.189	4.89	1.93	41.7	21.2	0.8152	0.2485	70 / 85 / 95		946 A	6.4 kA	36 kA
5	0.1819	4.621	5.50	2.16	33.1	16.8	1.028	0.3133		126/0.4	795 A	5.1 kA	28 kA
6	0.1620	4.115	6.17	2.43	26.3	13.3	1.296	0.3951	55 / 65 / 75		668 A	4.0 kA	23 kA
7	0.1443	3.665	6.93	2.73	20.8	10.5	1.634	0.4982		80/0.4	561 A	3.2 kA	18 kA
8	0.1285	3.264	7.78	3.06	16.5	8.37	2.061	0.6282	40 / 50 / 55		472 A	2.5 kA	14 kA
9	0.1144	2.906	8.74	3.44	13.1	6.63	2.599	0.7921		84/0.3	396 A	2.0 kA	11 kA
10	0.1019	2.588	9.81	3.86	10.4	5.26	3.277	0.9989	30 / 35 / 40	84/0.3	333 A	1.6 kA	8.9 kA
11	0.0907	2.305	11.0	4.34	8.23	4.17	4.132	1.260		56/0.3	280 A	1.3 kA	7.1 kA
12	0.0808	2.053	12.4	4.87	6.53	3.31	5.211	1.588	20 / 25 / 30		235 A	1.0 kA	5.6 kA
13	0.0720	1.828	13.9	5.47	5.18	2.62	6.571	2.003		50/0.25	198 A	798 A	4.5 kA
14	0.0641	1.628	15.6	6.14	4.11	2.08	8.286	2.525	15 / 20 / 25	64/0.2	166 A	633 A	3.5 kA
15	0.0571	1.450	17.5	6.90	3.26	1.65	10.45	3.184		30/0.25	140 A	502 A	2.8 kA
16	0.0508	1.291	19.7	7.75	2.58	1.31	13.17	4.016	— / — / 18	30/0.25	117 A	398 A	2.2 kA
17	0.0453	1.150	22.1	8.70	2.05	1.04	16.61	5.064		32/0.2	99 A	316 A	1.8 kA
18	0.0403	1.024	24.8	9.77	1.62	0.823	20.95	6.385	— / — / 14	24/0.2	83 A	250 A	1.4 kA
19	0.0359	0.912	27.9	11.0	1.29	0.653	26.42	8.051		24/0.2	70 A	198 A	1.1 kA
20	0.0320	0.812	31.3	12.3	1.02	0.518	33.31	10.15		16/0.2	58.5 A	158 A	882 A
21	0.0285	0.723	35.1	13.8	0.810	0.410	42.00	12.80		13/0.2	49 A	125 A	700 A
22	0.0253	0.644	39.5	15.5	0.642	0.326	52.96	16.14		7/0.25	41 A	99 A	551 A
23	0.0226	0.573	44.3	17.4	0.509	0.258	66.79	20.36			35 A	79 A	440 A
24	0.0201	0.511	49.7	19.6	0.404	0.205	84.22	25.67		1/0.5, 7/0.2, 30/0.1	29 A	62 A	348 A
25	0.0179	0.455	55.9	22.0	0.320	0.162	106.2	32.37			24 A	49 A	276 A
26	0.0159	0.405	62.7	24.7	0.254	0.129	133.9	40.81		1/0.4, 7/0.15	20 A	39 A	218 A
27	0.0142	0.361	70.4	27.7	0.202	0.102	168.9	51.47			17 A	31 A	174 A
28	0.0126	0.321	79.1	31.1	0.160	0.0810	212.9	64.90		7/0.12	14 A	24 A	137 A
29	0.0113	0.286	88.8	35.0	0.127	0.0642	268.5	81.84			12 A	20 A	110 A
30	0.0100	0.255	99.7	39.3	0.101	0.0509	338.6	103.2		1/0.25, 7/0.1	10 A	15 A	86 A
31	0.00893	0.227	112	44.1	0.0797	0.0404	426.9	130.1			9 A	12 A	69 A
32	0.00795	0.202	126	49.5	0.0632	0.0320	538.3	164.1		1/0.2, 7/0.08	7 A	10 A	54 A
33	0.00708	0.180	141	55.6	0.0501	0.0254	678.8	206.9			6 A	7.7 A	43 A
34	0.00630	0.160	159	62.4	0.0398	0.0201	856.0	260.9			5 A	6.1 A	34 A
35	0.00561	0.143	178	70.1	0.0315	0.0160	1079	329.0			4 A	4.8 A	27 A
36	0.00500*	0.127*	200*	78.7	0.0250	0.0127	1361	414.8			4 A	3.9 A	22 A
37	0.00445	0.113	225	88.4	0.0198	0.0100	1716	523.1			3 A	3.1 A	17 A
38	0.00397	0.101	252	99.3	0.0157	0.00797	2164	659.6			3 A	2.4 A	14 A
39	0.00353	0.0897	283	111	0.0125	0.00632	2729	831.8			2 A	1.9 A	11 A
40	0.00314	0.0799	318	125	0.00989	0.00501	3441	1049			1 A	1.5 A	8.5 A
AWG	Diameter		Turns of wire, no insulation		Area		Copper resistance		NEC copper wire ampacity with 60/75/90 °C insulation (A)	Approx. metric equivalents	Fusing current, copper
	(in)	(mm)	(per in)	(per cm)	(kcmil)	(mm²)	(Ω/km) (mΩ/m)	(Ω/kft) (mΩ/ft)			Preece, ~10 s	Onderdonk,
	(in)	(mm)	(per in)	(per cm)	(kcmil)	(mm²)	(Ω/km) (mΩ/m)	(Ω/kft) (mΩ/ft)			Preece, ~10 s	1 s	32 ms

*Exact (by definition)

In the North American electrical industry, conductors larger than 4/0 AWG are generally identified by the area in thousands of circular mils (kcmil), where 1 kcmil = 0.5067 mm². The next wire size larger than 4/0 has a cross section of 250 kcmil. A circular mil is the area of a wire one mil in diameter. One million circular mils is the area of a circle with 1000 mil = 1 inch diameter. An older abbreviation for one thousand circular mils is MCM.

Stranded wire AWG sizes

AWG gauges are also used to describe stranded wire. In this case, it describes a wire which is equal in cross-sectional area to the total of all the cross-sectional areas of the individual strands; the gaps between strands are not counted. When made with circular strands (see Circle packing), these gaps occupy about 10% of the wire area, thus requiring a wire about 5% thicker than equivalent solid wire.

Stranded wires are specified with three numbers, the overall AWG size, the number of strands, and the AWG size of a strand. The number of strands and the AWG of a strand are separated by a slash. For example, a 22 AWG 7/30 stranded wire is a 22 AWG wire made from seven strands of 30 AWG wire.

Nomenclature and abbreviations in electrical distribution

Main article: Electric power distribution

Alternate ways are commonly used in the electrical industry to specify wire sizes as AWG.

4 AWG (proper)
- #4 (the number sign is used as an abbreviation for "number")
- No. 4 (No. is used as an abbreviation for "number")
- No. 4 AWG
- 4 ga. (abbreviation for "gauge")
000 AWG (proper for large sizes)
- 3/0 (common for large sizes) Pronounced 3 aught
- 3/0 AWG
- #000
- #3/0

The industry also bundles common wire for use in electric power distribution in homes and businesses, identifying a bundle's wire size followed by the number of wires in the bundle. The most common type of distribution cable, NM-B, is generally implied:

#14/2 (also written "14-2") is a nonmetallic sheathed bundle of two solid 14 AWG wires. The insulation surrounding the two conductors is white and black. This sheath for 14 AWG cable is usually white when used for NM-B wiring intended for electrical distribution in a dry location. Newly manufactured cables without a separate ground wire (such as #14/2) are obsolete.
#12/2 with ground (also written "12-2 w/gnd") is a nonmetallic sheathed bundle of three solid 12 AWG wires having a bare ground in the middle of two insulated conductors in a flat-shaped NM-B yellow-colored sheath. The color is a North American industry standard for cables made since 2003, and aids identification.
#10/3 with ground (also written "10-3 w/gnd") is a nonmetallic sheathed bundle of four solid 10 AWG wires having a bare ground and three insulated conductors twisted into a round-shaped NM-B orange-colored sheath. The insulated conductors are black, white, and red. Some cable of this type may be flat to save copper.

USB data & charging cables

AWG is also used to describe USB cables, such as the common USB A to micro-B USB data / charging cables used to charge and sync smartphones and many other mobile devices. This is of particular concern to consumers, since thicker cables can potentially charge the device faster and with greater efficiency. When describing USB cables, AWG is specified with two numbers: First the gauge of the data transfer wires, followed by the gauge of the charging wires within the cable. Most USB cables are 28/28 AWG.^[11] However some cables that ship with tablets, and higher quality third-party cables, can be 28/24 AWG, 30/24, 28/21, etc, meaning the charging wires are thicker.^[11]

Pronunciation

AWG is colloquially referred to as gauge and the zeros in large wire sizes are referred to as aught /ˈɔːt/. Wire sized 1 AWG is referred to as "one gauge" or "No. 1" wire; similarly, smaller diameters are pronounced "x gauge" or "No. X" wire, where x is the positive integer AWG number. Consecutive AWG wire sizes larger than No. 1 wire are designated by the number of zeros:

No. 0, typically written 1/0 and is referred to as "one aught" wire
No. 00, typically written 2/0 and is referred to as "two aught" wire
No. 000, typically written 3/0 and is referred to as "three aught" wire,

and so on.

References

↑ "ASTM B258 - 14 Standard Specification for Standard Nominal Diameters and Cross-Sectional Areas of AWG Sizes of Solid Round Wires Used as Electrical Conductors". West Conshohocken: ASTM International. Archived from the original on 22 July 2014. Retrieved 22 March 2015. (subscription required)
↑ SteelNavel.com Body Piercing Jewelry Size Reference — illustrating the different ways that size is measured on different kinds of jewelry
↑ The logarithm to the base 92 can be computed using any other logarithm, such as common or natural logarithm, using log₉₂x = (log x)/(log 92).
↑ ASTM Standard B 258-02, page 4
↑ The result is roughly 2.0050, or one-quarter of one percent higher than 2
↑
Figure for solid copper wire at 68 °F, (Not in accordance to NEC Codebook 2014 Ch. 9, Table 8) computed based on 100% IACS conductivity of 58.0 MS/m, which agrees with multiple sources:
- Mark Lund, PowerStream Inc., American Wire Gauge table and AWG Electrical Current Load Limits, retrieved 2008-05-02 (although the ft/m conversion seems slightly erroneous)
- Belden Master Catalog, 2006, although data from there for gauges 35 and 37–40 seems obviously wrong.
High-purity oxygen-free copper can achieve up to 101.5% IACS conductivity; e.g., the Kanthal conductive alloys data sheet lists slightly lower resistances than this table.
↑ NFPA 70 National Electrical Code 2014 Edition. Table 310.15(B)(16) (formerly Table 310.16) page 70-161, Allowable ampacities of insulated conductors rated 0 through 2000 volts, 60°C through 90°C, not more than three current-carrying conductors in raceway, cable, or earth (directly buried) based on ambient temperature of 30°C. Extracts from NFPA 70 do not represent the full position of NFPA and the original complete Code must be consulted. In particular, the maximum permissible overcurrent protection devices may set a lower limit.
↑ The "Approximate stranded metric equivalents" column lists commonly available cables in the format "number of strands / diameter of individual strand (mm)" which is the common nomenclature describing cable construction within an overall cross-sectional area. Some common metric cables are midway between two AWG sizes. Cables sold in Europe are normally labeled according to the combined cross section of all strands in mm², which can be compared directly with the Area column.
↑ Computed using equations from H. Wayne Beaty; Donald G. Fink, eds. (2007), The Standard Handbook for Electrical Engineers (15th ed.), McGraw Hill, pp. 4–25, ISBN 0-07-144146-8
↑ Douglas Brooks (December 1998), "Fusing Current: When Traces Melt Without a Trace" (PDF), Printed Circuit Design 15 (12): 53
1 2 billcprice.com