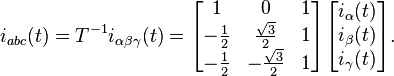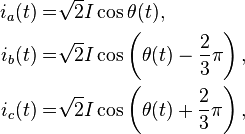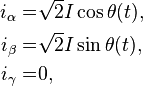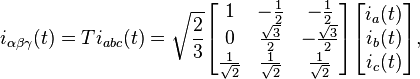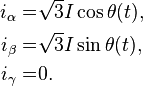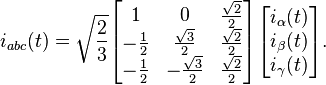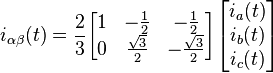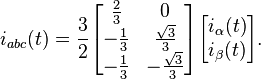Alpha–beta transformation
In electrical engineering, the alpha-beta (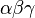 ) transformation (also known as the Clarke transformation) is a mathematical transformation employed to simplify the analysis of three-phase circuits. Conceptually it is similar to the dqo transformation. One very useful application of the
) transformation (also known as the Clarke transformation) is a mathematical transformation employed to simplify the analysis of three-phase circuits. Conceptually it is similar to the dqo transformation. One very useful application of the 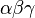 transformation is the generation of the reference signal used for space vector modulation control of three-phase inverters.
transformation is the generation of the reference signal used for space vector modulation control of three-phase inverters.
Definition
The 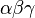 transform applied to three-phase currents, as used by Edith Clarke, is[1]
transform applied to three-phase currents, as used by Edith Clarke, is[1]
where 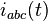 is a generic three-phase current sequence and
is a generic three-phase current sequence and 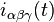 is the corresponding current sequence given by the transformation
is the corresponding current sequence given by the transformation  .
The inverse transform is:
.
The inverse transform is:
The above Clarke's transformation preserves the amplitude of the electrical variables which it is applied to. Indeed, consider a three-phase symmetric, direct, current sequence
where  is the RMS of
is the RMS of 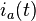 ,
, 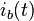 ,
, 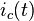 and
and 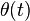 is the generic time-varying angle that can also be set to
is the generic time-varying angle that can also be set to 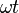 without loss of generality. Then, by applying
without loss of generality. Then, by applying  to the current sequence, it results
to the current sequence, it results
where the last equation holds since we have considered balanced currents. As it is shown in the above, the amplitudes of the currents in the 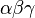 reference frame are the same of that in the natural reference frame.
reference frame are the same of that in the natural reference frame.
Power invariant transformation
The active and reactive powers computed in the Clark's domain with the transformation shown above are not the same of those computed in the standard reference frame. This happens because  is not unitary. In order to preserve the active and reactive powers one has, instead, to consider
is not unitary. In order to preserve the active and reactive powers one has, instead, to consider
which is a unitary matrix and the inverse coincides with its transpose.[2] In this case the amplitudes of the transformed currents are not the same of those in the standard reference frame, that is
Finally, the inverse trasformation in this case is
Simplified transformation
Since in a balanced system 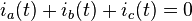 and thus
and thus 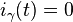 one can also consider the simplified transform[3]
one can also consider the simplified transform[3]
which is simply the original Clarke's transformation with the 3rd equation thrown away, and
Geometric Interpretation
The  transformation can be thought of as the projection of the three phase quantities (voltages or currents) onto two stationary axes, the alpha axis and the beta axis.
transformation can be thought of as the projection of the three phase quantities (voltages or currents) onto two stationary axes, the alpha axis and the beta axis.
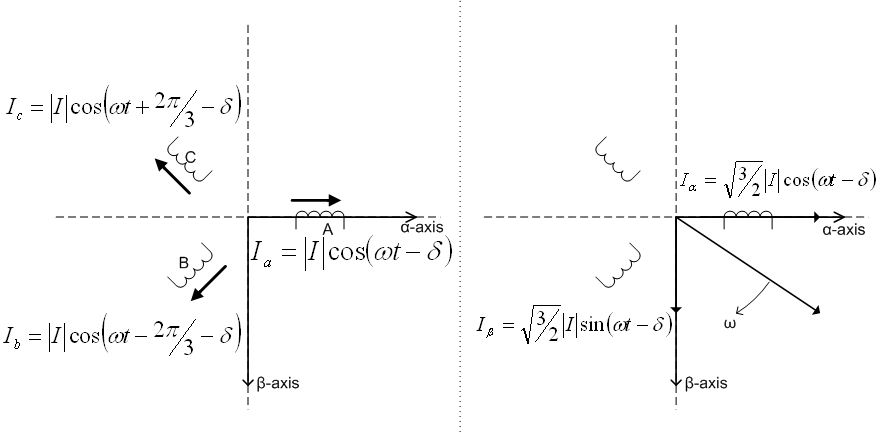
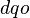 transform
transform
The 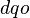 is conceptually similar to the
is conceptually similar to the 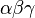 transform. Whereas the dqo transform is the projection of the phase quantities onto a rotating two-axis reference frame, the
transform. Whereas the dqo transform is the projection of the phase quantities onto a rotating two-axis reference frame, the 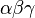 transform can be thought of as the projection of the phase quantities onto a stationary two-axis reference frame.
transform can be thought of as the projection of the phase quantities onto a stationary two-axis reference frame.
References
- ↑ W. C. Duesterhoeft, Max W. Schulz and Edith Clarke (July 1951). "Determination of Instantaneous Currents and Voltages by Means of Alpha, Beta, and Zero Components". Transactions of the American Institute of Electrical Engineers 70 (2): 1248–1255. doi:10.1109/T-AIEE.1951.5060554. ISSN 0096-3860.
- ↑ S. CHATTOPADHYAY, M. MITRA, S. SENGUPTA (2008). "Area Based Approach for Three Phase Power Quality Assessment in Clarke Plane" (PDF). Journal of Electrical Systems 04 (01): 62. Retrieved 2012-04-26.
- ↑ F. Tahri, A.Tahri, Eid A. AlRadadi and A. Draou Senior, "Analysis and Control of Advanced Static VAR compensator Based on the Theory of the Instantaneous Reactive Power," presented at ACEMP, Bodrum, Turkey, 2007.