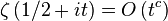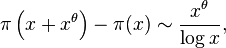Albert Ingham

Albert Ingham
Born Albert Edward Ingham
(1900-04-03)3 April 1900
Northampton
Died 6 September 1967(1967-09-06) (aged 67)
Institutions University of Cambridge
Alma mater Trinity College, Cambridge
Doctoral students Wolfgang Fuchs
C. Haselgrove
Christopher Hooley
William Pennington
Robert Rankin[1]
Influences John Edensor Littlewood[2]
Notable awards Smith's Prize (1921)[2]
Fellow of the Royal Society[3]
Notes
Erdős Number: 1

Albert Edward Ingham FRS (3 April 1900 – 6 September 1967) was an English mathematician.[4]

Education

Ingham was born in Northampton. He went to Stafford Grammar School and Trinity College, Cambridge.[2]

Research

Ingham supervised the Ph.D.s of C. Brian Haselgrove, Wolfgang Fuchs and Christopher Hooley.[1] Ingham died in Chamonix, France.

Ingham proved in 1937[5] that if

\zeta\left(1/2+it\right)=O\left(t^c\right)

for some positive constant c, then

\pi\left(x+x^\theta\right)-\pi(x)\sim\frac{x^\theta}{\log x},

for any θ > (1+4c)/(2+4c). Here ζ denotes the Riemann zeta function and π the prime-counting function.

Using the best published value for c at the time, an immediate consequence of his result was that

gn < pn5/8,

where pn the n-th prime number and gn = pn+1 − pn denotes the n-th prime gap.

References

  1. 1 2 Albert Ingham at the Mathematics Genealogy Project
  2. 1 2 3 O'Connor, John J.; Robertson, Edmund F., "Albert Ingham", MacTutor History of Mathematics archive, University of St Andrews.
  3. ↑ Burkill, J. C. (1968). "Albert Edward Ingham 1900-1967". Biographical Memoirs of Fellows of the Royal Society 14: 271–226. doi:10.1098/rsbm.1968.0012.
  4. ↑ The Distribution of Prime Numbers, Cambridge University Press, 1932 (Reissued with a foreword by R. C. Vaughan in 1990)
  5. ↑ Ingham, A. E. (1937). "On the Difference Between Consecutive Primes". The Quarterly Journal of Mathematics: 255. doi:10.1093/qmath/os-8.1.255.


This article is issued from Wikipedia - version of the Sunday, August 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.