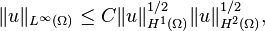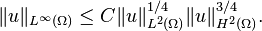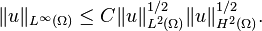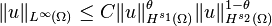Agmon's inequality
In mathematical analysis, Agmon's inequalities, named after Shmuel Agmon,[1] consist of two closely related interpolation inequalities between the Lebesgue space  and the Sobolev spaces
and the Sobolev spaces 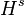 . It is useful in the study of partial differential equations.
. It is useful in the study of partial differential equations.
Let 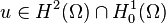 where
where 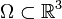 . Then Agmon's inequalities in 3D state that there exists a constant
. Then Agmon's inequalities in 3D state that there exists a constant 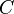 such that
such that
and
In 2D, the first inequality still holds, but not the second: let 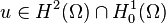 where
where  . Then Agmon's inequality in 2D states that there exists a constant
. Then Agmon's inequality in 2D states that there exists a constant 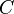 such that
such that
For the  -dimensional case, choose
-dimensional case, choose  and
and 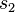 such that
such that 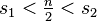 . Then, if
. Then, if 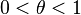 and
and 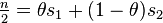 , the following inequality holds for any
, the following inequality holds for any 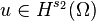
See also
Notes
- ↑ Lemma 13.2, in: Agmon, Shmuel, Lectures on Elliptic Boundary Value Problems, AMS Chelsea Publishing, Providence, RI, 2010. ISBN 978-0-8218-4910-1.
References
- Agmon, Shmuel (2010). Lectures on elliptic boundary value problems. , Providence, RI: AMS Chelsea Publishing. ISBN 978-0-8218-4910-1.
- Foias, Ciprian; Manley, O.; Rosa, R.; Temam, R. (2001). Navier-Stokes Equations and Turbulence. Cambridge: Cambridge University Press. ISBN 0-521-36032-3.
This article is issued from Wikipedia - version of the Saturday, May 02, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.