Admissible ordinal

In set theory, an ordinal number α is an admissible ordinal if Lα is an admissible set (that is, a transitive model of Kripke–Platek set theory); in other words, α is admissible when α is a limit ordinal and Lα⊧Σ0-collection.[1][2]

The first two admissible ordinals are ω and 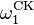\omega_1^{\mathrm{CK}} (the least non-recursive ordinal, also called the Church–Kleene ordinal).[2] Any regular uncountable cardinal is an admissible ordinal.

By a theorem of Sacks, the countable admissible ordinals are exactly those constructed in a manner similar to the Church-Kleene ordinal, but for Turing machines with oracles.[1] One sometimes writes 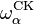\omega_\alpha^{\mathrm{CK}} for the \alpha-th ordinal which is either admissible or a limit of admissibles; an ordinal which is both is called recursively inaccessible.[3] There exists a theory of large ordinals in this manner that is highly parallel to that of (small) large cardinals (one can define recursively Mahlo ordinals, for example).[4] But all these ordinals are still countable. Therefore, admissible ordinals seem to be the recursive analogue of regular cardinal numbers.

Notice that α is an admissible ordinal if and only if α is a limit ordinal and there does not exist a γ<α for which there is a Σ1(Lα) mapping from γ onto α. If M is a standard model of KP, then the set of ordinals in M is an admissible ordinal.

See also

References

  1. 1 2 Friedman, Sy D. (1985), "Fine structure theory and its applications", Recursion theory (Ithaca, N.Y., 1982), Proc. Sympos. Pure Math. 42, Amer. Math. Soc., Providence, RI, pp. 259–269, doi:10.1090/pspum/042/791062, MR 791062. See in particular p. 265.
  2. 1 2 Fitting, Melvin (1981), Fundamentals of generalized recursion theory, Studies in Logic and the Foundations of Mathematics 105, North-Holland Publishing Co., Amsterdam-New York, p. 238, ISBN 0-444-86171-8, MR 644315.
  3. ↑ Friedman, Sy D. (2010), "Constructibility and class forcing", Handbook of set theory. Vols. 1, 2, 3, Springer, Dordrecht, pp. 557–604, doi:10.1007/978-1-4020-5764-9_9, MR 2768687. See in particular p. 560.
  4. ↑ Kahle, Reinhard; Setzer, Anton (2010), "An extended predicative definition of the Mahlo universe", Ways of proof theory, Ontos Math. Log. 2, Ontos Verlag, Heusenstamm, pp. 315–340, MR 2883363.
This article is issued from Wikipedia - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.