Adjoint equation

An adjoint equation is a linear differential equation, usually derived from its primal equation using integration by parts. Gradient values with respect to a particular quantity of interest can be efficiently calculated by solving the adjoint equation. Methods based on solution of adjoint equations are used in wing shape optimization, fluid flow control and uncertainty quantification. For example 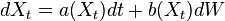$dX_t = a(X_t)dt + b(X_t)dW$ this is an Itō stochastic differential equation. Now by using Euler scheme, we integrate the parts of this equation and get another equation, 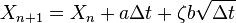$X_{n+1} = X_n + a \Delta t + \zeta b \sqrt{\Delta t}$ , here 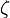$\zeta$ is a random variable, later one is an adjoint equation.

References

Jameson, Antony (1988). "Aerodynamic Design via Control Theory". Journal of Scientific Computing 3 (3).

This article is issued from Wikipedia - version of the Thursday, June 05, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Adjoint equation

See also

References