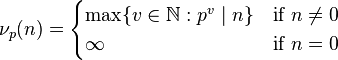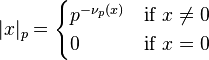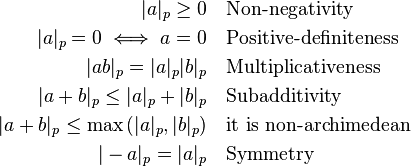p-adic order

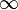In number theory, for a given prime number $p$ , the $p$ -adic order or $p$ -adic additive valuation of a non-zero integer $n$ is the highest exponent ν such that $p$ ^ν divides $n$ . The $p$ -adic valuation of $0$ is defined to be $\infty$ . It is commonly abbreviated ν_$p$( $n$ ). If $n/d$ is a rational number in lowest terms, so that $n$ and $d$ are relatively prime, then ν_$p$( $n/d$ ) is equal to ν_$p$( $n$ ) if $p$ divides $n$ , or -ν_$p$( $d$ ) if $p$ divides $d$ , or to 0 if it divides neither one. The most important application of the p-adic order is in constructing the field of p-adic numbers. It is also applied toward various more elementary topics, such as the distinction between singly and doubly even numbers.^[1]

Distribution of natural numbers by their 2-adic order, labeled with corresponding powers of two in decimal. Zero always has an infinite order

Definition and Properties

Integers

Let $p$ be a prime in Z. The $p$ -adic order or $p$ -adic valuation for Z is defined as^[2] 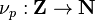$\nu_p:\textbf{Z} \to \textbf{N}$

\nu_p(n)= \begin{cases} \mathrm{max}\{v\in\mathbb{N}:p^v \mid n\} & \text{if } n \neq 0\\ \infty & \text{if } n=0 \end{cases}

Rational Numbers

The $p$ -adic order can be extended into the rational numbers. We can define^[3] 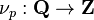$\nu_p:\textbf{Q} \to \textbf{Z}$

\nu_p\left(\frac{a}{b}\right)=\nu_p(a)-\nu_p(b).

Some properties are:

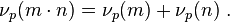
\nu_p(m\cdot n)= \nu_p(m) + \nu_p(n)~.

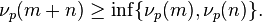\nu_p(m+n)\geq \inf\{ \nu_p(m), \nu_p(n)\}.

Moreover, if

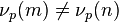\nu_p(m)\ne \nu_p(n)

, then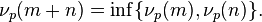

\nu_p(m+n)= \inf\{ \nu_p(m), \nu_p(n)\}.

where $\inf$ is the Infimum (i.e. the smaller of the two)

p-adic Norm

From our definition of the $p$ -adic order, we can define the so-called $p$ -adic norm. (It is not actually a norm because it does not satisfy the requirement of homogeneity, but it is an absolute value.) The $p$ -adic norm of Q is defined as $|\,\cdot\,|_p: \textbf{Q} \to \textbf{R}$

|x|_p = \begin{cases} p^{-\nu_p(x)} & \text{if } x \neq 0\\ 0 & \text{if } x=0 \end{cases}

Some properties of the $p$ -adic norm:

\begin{align} |a|_p \geq 0 & \quad \text{Non-negativity}\\ |a|_p = 0 \iff a = 0 & \quad \text{Positive-definiteness}\\ |ab|_p = |a|_p|b|_p & \quad \text{Multiplicativeness}\\ |a+b|_p \leq |a|_p + |b|_p & \quad \text{Subadditivity}\\ |a+b|_p \leq \max\left(|a|_p, |b|_p\right) & \quad \text{it is non-archimedean}\\ |-a|_p = |a|_p & \quad \text{Symmetry} \end{align}

A metric space can be formed on the set Q with a (non-archimedean, translation invariant) metric defined by 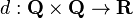$d:\textbf{Q}\times\textbf{Q} \to \textbf{R}$

d(x,y)=|x-y|_p.

References

↑ David S. Dummit; Richard M. Foote (2003). Abstract Algebra (3rd ed.). Wiley. ISBN 0-471-43334-9.
↑ Ireland, K., Rosen, M. (2000). A Classical Introduction to Modern Number Theory. Springer-Verlag New York. Inc., p. 3
↑ Khrennikov, A., Nilsson, M. (2004). P-adic Deterministic and Random Dynamics., Kluwer Academic Publishers, p. 9

This article is issued from Wikipedia - version of the Friday, November 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.