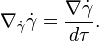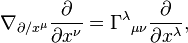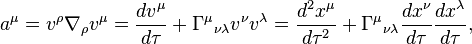Acceleration (differential geometry)

In mathematics and physics, acceleration is the rate of change of velocity of a curve with respect to a given linear connection. This operation provides us with a measure of the rate and direction of the "bend".[1][2]

Formal definition

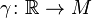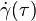Consider a differentiable manifold M with a given connection \Gamma. Let \gamma \colon\R \to M be a curve in M with tangent vector, i.e. velocity, {\dot\gamma}(\tau), with parameter \tau.

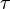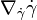The acceleration vector of \gamma is defined by \nabla_{\dot\gamma}{\dot\gamma} , where \nabla denotes the covariant derivative associated to \Gamma.

It is a covariant derivative along \gamma, and it is often denoted by

\nabla_{\dot\gamma}{\dot\gamma} =\frac{\nabla\dot\gamma}{d\tau}.

With respect to an arbitrary coordinate system 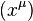(x^{\mu}), and with 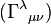(\Gamma^{\lambda}{}_{\mu\nu}) being the components of the connection (i.e., covariant derivative 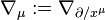\nabla_{\mu}:=\nabla_{\partial/x^\mu}) relative to this coordinate system, defined by

\nabla_{\partial/x^\mu}\frac{\partial}{\partial x^{\nu}}= \Gamma^{\lambda}{}_{\mu\nu}\frac{\partial}{\partial x^{\lambda}},

for the acceleration vector field 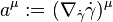a^{\mu}:=(\nabla_{\dot\gamma}{\dot\gamma})^{\mu} one gets:

a^{\mu}=v^{\rho}\nabla_{\rho}v^{\mu} =\frac{dv^{\mu}}{d\tau}+ \Gamma^{\mu}{}_{\nu\lambda}v^{\nu}v^{\lambda}= \frac{d^2x^{\mu}}{d\tau^2}+ \Gamma^{\mu}{}_{\nu\lambda}\frac{dx^{\nu}}{d\tau}\frac{dx^{\lambda}}{d\tau},

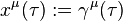where x^{\mu}(\tau):= \gamma^{\mu}(\tau) is the local expression for the path \gamma, and v^{\rho}:=({\dot\gamma})^{\rho}.

The concept of acceleration is a covariant derivative concept. In other words, in order to define acceleration an additional structure on M must be given.

See also

Notes

  1. ↑ Friedman, M. (1983). Foundations of Space-Time Theories. Princeton: Princeton University Press. p. 38. ISBN 0-691-07239-6.
  2. ↑ Benn, I.M.; Tucker, R.W. (1987). An Introduction to Spinors and Geometry with Applications in Physics. Bristol and New York: Adam Hilger. p. 203. ISBN 0-85274-169-3.

References

This article is issued from Wikipedia - version of the Monday, January 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.