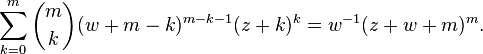Abel's binomial theorem

Abel's binomial theorem, named after Niels Henrik Abel, is a mathematical identity involving sums of binomial coefficients. It states the following:

\sum_{k=0}^m \binom{m}{k} (w+m-k)^{m-k-1}(z+k)^k=w^{-1}(z+w+m)^m.

Example

m = 2

\begin{align} & {} \quad \binom{2}{0}(w+2)^1(z+0)^0+\binom{2}{1}(w+1)^0(z+1)^1+\binom{2}{2}(w+0)^{-1}(z+2)^2 \\ & = (w+2)+2(z+1)+\frac{(z+2)^2}{w} \\ & = \frac{(z+w+2)^2}{w}. \end{align}

See also

References

This article is issued from Wikipedia - version of the Saturday, November 15, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.