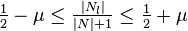AVL tree
| AVL tree | ||
|---|---|---|
| Type | Tree | |
| Invented | 1962 | |
| Invented by | Georgy Adelson-Velsky and Evgenii Landis | |
| Time complexity in big O notation | ||
| Average | Worst case | |
| Space | O(n) | O(n) |
| Search | O(log n)[1] | O(log n)[1] |
| Insert | O(log n)[1] | O(log n)[1] |
| Delete | O(log n)[1] | O(log n)[1] |

In computer science, an AVL tree (Georgy Adelson-Velsky and Evgenii Landis' tree, named after the inventors) is a self-balancing binary search tree. It was the first such data structure to be invented.[2] In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
The AVL tree is named after its two Soviet inventors, Georgy Adelson-Velsky and Evgenii Landis, who published it in their 1962 paper "An algorithm for the organization of information".[3]
AVL trees are often compared with red-black trees because both support the same set of operations and take O(log n) time for the basic operations. For lookup-intensive applications, AVL trees are faster than red-black trees because they are more rigidly balanced.[4] Similar to red-black trees, AVL trees are height-balanced. Both are in general not weight-balanced nor μ-balanced for any 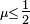 ;[5] that is, sibling nodes can have hugely differing numbers of descendants.
;[5] that is, sibling nodes can have hugely differing numbers of descendants.
Operations

Basic operations of an AVL tree involve carrying out the same actions as would be carried out on an unbalanced binary search tree, but modifications are followed by zero or more operations called tree rotations, which help to restore the height balance of the subtrees.
Searching
Searching for a key in an AVL tree can be done the same way as that of a normal unbalanced binary search tree.
Traversal
Once a node has been found in a balanced tree, the next or previous nodes can be explored in amortized constant time. Some instances of exploring these "nearby" nodes require traversing up to log(n) links (particularly when moving from the rightmost leaf of the root's left subtree to the root or from the root to the leftmost leaf of the root's right subtree; in the example AVL tree, moving from node 14 to the next but one node 19 takes 4 steps). However, exploring all n nodes of the tree in this manner would use each link exactly twice: one traversal to enter the subtree rooted at that node, another to leave that node's subtree after having explored it. And since there are n−1 links in any tree, the amortized cost is found to be 2×(n−1)/n, or approximately 2.
Insertion
After inserting a node, it is necessary to check each node starting with the subject node and advancing up to the root for consistency with the invariants of AVL trees: this is called "retracing". This is achieved by considering the balance factor of each node, which is defined as the difference in heights of the left and right subtrees.

Thus the balance factor of any node of an AVL tree is in the integer range [-1,+1]. This balance factor is stored in the node, but may have to be corrected after an insertion or a deletion, which is also done during retracing. Since with a single insertion the height of an AVL subtree cannot increase by more than one, the temporarily recomputed balance factor of a node after an insertion will be in the range [−2,+2]. For each node checked, if the recomputed balance factor remains in the range [−1,+1] no rotations are necessary. However, if the recomputed balance factor becomes less than −1 or greater than +1, the subtree rooted at this node is unbalanced, and a rotation is needed.
- Description of the Rotations
Let us first assume the balance factor of a node P is 2 (as opposed to the other possible unbalanced value −2). This case is depicted in the left column of the illustration with P:=5. We then look at the left subtree (the higher one), N its root. If this subtree does not lean to the right - i.e. N has balance factor 1 (or, when deletion also 0) - we can rotate the tree (rooted by 5) to the right to get a balanced tree. This is labelled as the "Left Left Case" in the illustration with N:=4. If the subtree does lean to the right - i.e. N:=3 has balance factor −1 - we first rotate the subtree to the left and end up the previous case. This second case is labelled as "Left Right Case" in the illustration.
If the balance factor of the node P is −2 (this case is depicted in the right column of the illustration P:=3) we can mirror the above algorithm. I.e. if the root N of the (higher) right subtree has balance factor −1 (or, when deletion also 0) we can rotate the whole tree to the left to get a balanced tree. This is labelled as the "Right Right Case" in the illustration with N:=4. If the root N:=5 of the right subtree has balance factor 1 ("Right Left Case") we can rotate the subtree to the right to end up in the "Right Right Case".
The whole retracing loop for an insertion looks like this:
// N is the child of P whose height increases by 1.
do {
// balance_factor(P) has not yet been updated!
if (N == left_child(P)) { // the left subtree increases
if (balance_factor(P) == 1) { // The left column in the picture
// ==> the temporary balance_factor(P) == 2 ==> rebalancing is required.
if (balance_factor(N) == -1) { // Left Right Case
rotate_left(N); // Reduce to Left Left Case
}
// Left Left Case
rotate_right(P);
break; // Leave the loop
}
if (balance_factor(P) == -1) {
balance_factor(P) = 0; // N’s height increase is absorbed at P.
break; // Leave the loop
}
balance_factor(P) = 1; // Height increases at P
} else { // N == right_child(P), the child whose height increases by 1.
if (balance_factor(P) == -1) { // The right column in the picture
// ==> the temporary balance_factor(P) == -2 ==> rebalancing is required.
if (balance_factor(N) == 1) { // Right Left Case
rotate_right(N); // Reduce to Right Right Case
}
// Right Right Case
rotate_left(P);
break; // Leave the loop
}
if (balance_factor(P) == 1) {
balance_factor(P) = 0; // N’s height increase is absorbed at P.
break; // Leave the loop
}
balance_factor(P) = -1; // Height increases at P
}
N = P;
P = parent(N);
} while (P != null); // Possibly up to the root
After a rotation a subtree has the same height as before, so retracing can stop. In order to restore the balance factors of all nodes, first observe that all nodes requiring correction lie along the path used during the initial insertion. If the above procedure is applied to nodes along this path, starting from the bottom (i.e. the inserted node), then every node in the tree will again have a balance factor of −1, 0, or 1.
The time required is O(log n) for lookup, plus a maximum of O(log n) retracing levels on the way back to the root, so the operation can be completed in O(log n) time.
Deletion
Let node X be the node with the value we need to delete, and let node Y be a node in the tree we need to find to take node X's place, and let node Z be the actual node we take out of the tree.
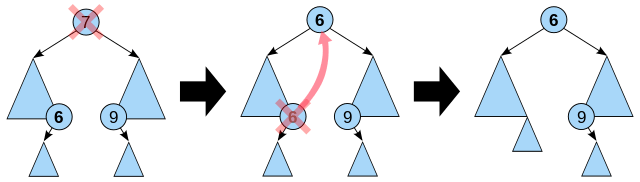
Steps to consider when deleting a node in an AVL tree are the following:
- If node X is a leaf or has only one child, skip to step 5 with Z:=X.
- Otherwise, determine node Y by finding the largest node in node X's left subtree (the in-order predecessor of X − it does not have a right child) or the smallest in its right subtree (the in-order successor of X − it does not have a left child).
- Exchange all the child and parent links of node X with those of node Y. In this step, the in-order sequence between nodes X and Y is temporarily disturbed, but the tree structure doesn't change.
- Choose node Z to be all the child and parent links of old node Y = those of new node X.
- If node Z has a subtree (which then is a leaf), attach it to Z's parent.
- If node Z was the root (its parent is null), update root.
- Delete node Z.
- Retrace the path back up the tree (starting with node Z's parent) to the root, adjusting the balance factors as needed.
Since with a single deletion the height of an AVL subtree cannot decrease by more than one, the temporary balance factor of a node will be in the range from −2 to +2.
If the balance factor becomes ±2 then the subtree is unbalanced and needs to be rotated. The various cases of rotations are depicted in section "Insertion".
The whole retracing loop for a deletion looks like this:
// N is the child of P whose height decreases by 1.
do {
// balance_factor(P) has not yet been updated!
if (N == right_child(P)) { // the right subtree decreases
if (balance_factor(P) == 1) { // The left column in the picture
// ==> the temporary balance_factor(P) == 2 ==> rebalancing is required.
S = left_child(P); // Sibling of N
B = balance_factor(S);
if (B == -1) { // Left Right Case
rotate_left(S); // Reduce to Left Left Case
}
// Left Left Case
rotate_right(P);
if (B == 0) // (in the picture the small blue (0) at node 4)
break; // Height does not change: Leave the loop
}
if (balance_factor(P) == 0) {
balance_factor(P) = 1; // N’s height decrease is absorbed at P.
break; // Leave the loop
}
balance_factor(P) = 0; // Height decreases at P
} else { // N == left_child(P), the child whose height decreases by 1.
if (balance_factor(P) == -1) { // The right column in the picture
// ==> the temporary balance_factor(P) == -2 ==> rebalancing is required.
S = right_child(P); // Sibling of N
B = balance_factor(S);
if (B == 1) { // Right Left Case
rotate_right(S); // Reduce to Right Right Case
}
// Right Right Case
rotate_left(P);
if (B == 0) // (in the picture the small blue (0) at node 4)
break; // Height does not change: Leave the loop
}
if (balance_factor(P) == 0) {
balance_factor(P) = -1; // N’s height decrease is absorbed at P.
break; // Leave the loop
}
balance_factor(P) = 0; // Height decreases at P
}
N = P;
P = parent(N);
} while (P != null); // Possibly up to the root
The retracing can stop if the balance factor becomes ±1 indicating that the height of that subtree has remained unchanged. This can also result from a rotation when the higher child tree has a balance factor of 0.
If the balance factor becomes 0 then the height of the subtree has decreased by one and the retracing needs to continue. This can also result from a rotation.
The time required is O(log n) for lookup, plus a maximum of O(log n) retracing levels on the way back to the root, so the operation can be completed in O(log n) time.
Comparison to other structures
Both AVL trees and red-black trees are self-balancing binary search trees and they are very similar mathematically. The operations to repair the balance of the trees are different, but both take O(1) at one level. However with both trees, there is a certain chance ≤ 0.5 that the balancing rules will be violated at the next or next but one level higher up to the root. Thus, on the average, where the number of levels being repaired is ≈ 1 or 2, rebalancing consumes O(1), and in the worst case it is in O(log n) when repair happens to take place at each level up to the root.
A first difference between the two is the limiting height.
For a tree of size  :
:
- An AVL tree's height is strictly less than:[6][7]
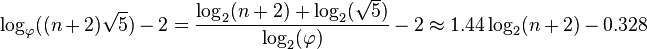
- where
 is the golden ratio.
is the golden ratio.
- A red-black tree's height is at most
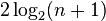 [8]
[8]
As a consequence, AVL trees are more rigidly balanced than red-black trees,[9] leading to faster retrieval but maybe slower insertion and removal. Performance comparisons can be found in Ben Pfaff.[4] His results show in 79 measurement runs the similarity of AVL trees (AVL) and red-black trees (RB) with relations AVL⁄RB between 0.677 and 1.077, median ≈0.947, and geometric mean ≈0.910.
Another difference is pointed out by Mehlhorn[10] (p. 165): "AVL trees do not support constant amortized update costs", whereas red-black trees do (p. 158).
See also
- Trees
- Tree rotation
- Red-black tree
- Splay tree
- Scapegoat tree
- B-tree
- T-tree
- WAVL tree
- List of data structures
References
- 1 2 3 4 5 6 Eric Alexander. "AVL Trees".
- ↑ Robert Sedgewick, Algorithms, Addison-Wesley, 1983, ISBN 0-201-06672-6, page 199, chapter 15: Balanced Trees.
- ↑ Georgy Adelson-Velsky, G.; Evgenii Landis (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences (in Russian) 146: 263–266. English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962.
- 1 2 Pfaff, Ben (June 2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University.
- ↑ AVL trees are not weight-balanced? (meaning: AVL trees are not μ-balanced?)
Thereby: A Binary Tree is called -balanced, with
-balanced, with 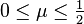 , if for every node
, if for every node  , the inequality
, the inequality
 is minimal with this property.
is minimal with this property.  is the number of nodes below the tree with
is the number of nodes below the tree with  as root (including the root) and
as root (including the root) and  is the left child node of
is the left child node of  .
. -
- ↑ Burkhard, Walt (Spring 2012). "AVL Dictionary Data Type Implementation". Advanced Data Structures (PDF). La Jolla: A.S. Soft Reserves, UC San Diego. p. 103. External link in
|publisher=(help) - ↑ Knuth, Donald E. (2000). Sorting and searching (2. ed., 6. printing, newly updated and rev. ed.). Boston [u.a.]: Addison-Wesley. p. 460. ISBN 0-201-89685-0.
- ↑ Proof of asymptotic bounds
- ↑ In fact, every AVL tree can be colored red-black.
- ↑ Mehlhorn, Kurt; Sanders, Peter (2008). Algorithms and Data Structures. The Basic Toolbox. (PDF). Springer, Berlin/Heidelberg. pp. 154–165. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3.
Further reading
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 458–475 of section 6.2.3: Balanced Trees.
External links
| The Wikibook Algorithm Implementation has a page on the topic of: AVL tree |
| Wikimedia Commons has media related to AVL-trees. |
- xdg library by Dmitriy Vilkov: Serializable straight C-implementation could easily be taken from this library under GNU-LGPL and AFL v2.0 licenses.
- Description from the Dictionary of Algorithms and Data Structures
- Python Implementation
- Single C header file by Ian Piumarta
- AVL Tree Demonstration
- AVL tree applet – all operations
- Fast and efficient implementation of AVL Trees
- PHP Implementation
- AVL Threaded Tree PHP Implementation
- C++ implementation which can be used as an array
- Self balancing AVL tree with Concat and Split operations
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||