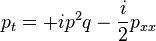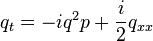AKNS system
In mathematics, the AKNS system is an integrable system of partial differential equations, introduced by and named after Mark J. Ablowitz, David J. Kaup, and Alan C. Newell et al. (1974).
Definition
The AKNS system is a pair of two partial differential equations for two complex-valued functions p and q of 2 variables t and x:
If p and q are complex conjugates this reduces to the nonlinear Schrödinger equation.
Huygens' principle applied to the Dirac operator gives rise to the AKNS hierarchy.[1]
See also
References
- Ablowitz, Mark J.; Kaup, David J.; Newell, Alan C.; Segur, Harvey (1974), "The inverse scattering transform-Fourier analysis for nonlinear problems", Studies in Appl. Math. 53 (4): 249–315, MR 0450815
- ↑ Fabio A. C. C. Chalub1 and Jorge P. Zubelli, "Huygens’ Principle for Hyperbolic Operators and Integrable Hierarchies"
This article is issued from Wikipedia - version of the Sunday, January 17, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.