8-8 duoprism

Uniform 8-8 duoprism Schlegel diagram
Type	Uniform duoprism
Schläfli symbol	{8}×{8} = {8}2
Coxeter diagrams
Cells	16 octagonal prisms
Faces	64 squares, 16 octagons
Edges	128
Vertices	64
Vertex figure	Tetragonal disphenoid
Symmetry	[[8,2,8]] = [16,2+,16], order 512
Dual	8-8 duopyramid
Properties	convex, vertex-uniform, facet-transitive

In geometry of 4 dimensions, a 8-8 duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two octagons.

It has 64 vertices, 128 edges, 80 faces (64 squares, and 16 octagons), in 16 octagonal prism cells. It has Coxeter diagram , and symmetry [[8,2,8]], order 512.

Images

A perspective view of half of the octagonal prisms along one direction, alternately colored.

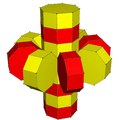
The uniform 8-8 duoprism can be constructed from [8]×[8] or [4]×[4] symmetry, order 256 or 64, with extended symmetry doubling these with a 2-fold rotation that maps the two orientations of prisms together. These can be expressed by 4 permutations of uniform coloring of the octahedral prism cells.

Uniform colored nets

[[8,2,8]], order 512	[8,2,8], order 256	[[4,2,4]], order 128	[4,2,4], order 64
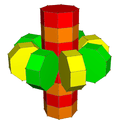{8}2	{8}×{8}	t{4}2	t{4}×t{4}

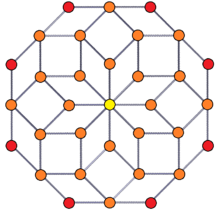
Seen in a skew 2D orthogonal projection, it has the same vertex positions as the hexicated 7-simplex, except for a center vertex. The projected rhombi and squares are also shown in the Ammann–Beenker tiling.

8-8 duoprism	4-4 duoprism	Hexicated 7-simplex
Ammann–Beenker tiling	{8/3} octagrams
8-8 duoprism

8-8 duopyramid

8-8 duopyramid
Type	Uniform dual duopyramid
Schläfli symbol	{8}+{8} = 2{8}
Coxeter diagrams
Cells	64 tetragonal disphenoids
Faces	128 isosceles triangles
Edges	80 (64+16)
Vertices	16 (8+8)
Symmetry	[[8,2,8]] = [16,2+,16], order 512
Dual	8-8 duoprism
Properties	convex, vertex-uniform, facet-transitive

The dual of a 8-8 duoprism is called a 8-8 duopyramid. It has 64 tetragonal disphenoid cells, 128 triangular faces, 80 edges, and 16 vertices.

orthogonal projections

Skew	[16]

See also

• 3-3 duoprism
• 3-4 duoprism
• 5-5 duoprism
• Tesseract (4-4 duoprism)
• Convex regular 4-polytope
• Duocylinder

Notes

References

• Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
  • Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• Olshevsky, George, Duoprism at Glossary for Hyperspace.
  • Catalogue of Convex Polychora, section 6, George Olshevsky.

External links

• The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
• Polygloss - glossary of higher-dimensional terms
• Exploring Hyperspace with the Geometric Product