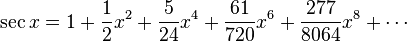277 (number)
| ||||
|---|---|---|---|---|
| Cardinal | two hundred seventy-seven | |||
| Ordinal |
277th (two hundred and seventy-seventh) | |||
| Factorization | 277 | |||
| Prime | yes | |||
| Roman numeral | CCLXXVII | |||
| Binary | 1000101012 | |||
| Ternary | 1010213 | |||
| Quaternary | 101114 | |||
| Quinary | 21025 | |||
| Senary | 11416 | |||
| Octal | 4258 | |||
| Duodecimal | 1B112 | |||
| Hexadecimal | 11516 | |||
| Vigesimal | DH20 | |||
| Base 36 | 7P36 | |||
277 (read as two hundred and seventy-seven) is the natural number following 276 and preceding 278.
Mathematical properties
277 is the 59th prime number, and is a regular prime.[1] It is the smallest prime p such that the sum of the inverses of the primes up to p is greater than two.[2] Since 59 is itself prime, 277 is a super-prime.[3] 59 is also a super-prime (it is the 17th prime), as is 17 (the 7th prime). However, 7 is the fourth prime number, and 4 is not prime. Thus, 277 is a super-super-super-prime but not a super-super-super-super-prime.[4] It is the largest prime factor of the Euclid number 510511 = 2 × 3 × 5 × 7 × 11 × 13 × 17 + 1.[5]
As a member of the lazy caterer's sequence, 277 counts the maximum number of pieces obtained by slicing a pancake with 23 straight cuts.[6] 277 is also a Perrin number, and as such counts the number of maximal independent sets in an icosagon.[7][8] There are 277 ways to tile a 3 × 8 rectangle with integer-sided squares,[9] and 277 degree-7 monic polynomials with integer coefficients and all roots in the unit disk.[10] On an infinite chessboard, there are 277 squares that a knight can reach from a given starting position in exactly six moves.[11]
277 appears as the numerator of the fifth term of the Taylor series for the secant function:[12]
Since no number added to the sum of its digits generates 277, it is a self number. The next prime self number is not reached until 367.[13]
Two hundred and seventy-seven is also:
- The length of the Grand Canyon in river miles, beginning at Lees Ferry (mile 0) and ending at the Grand Wash Cliffs (mile 277).[14]
References
- ↑ "Sloane's A007703 : Regular primes", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A016088 : a(n) = smallest prime p such that Sum_{ primes q = 2, ..., p} 1/q exceeds n", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A006450 : Primes with prime subscripts", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Fernandez, Neil (1999), An order of primeness, F(p).
- ↑ "Sloane's A002585 : Largest prime factor of 1 + (product of first n primes)", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A000124 : Central polygonal numbers (the Lazy Caterer's sequence): n(n+1)/2 + 1; or, maximal number of pieces formed when slicing a pancake with n cuts", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A001608 : Perrin sequence (or Ondrej Such sequence): a(n) = a(n-2) + a(n-3)", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Füredi, Z. (1987), "The number of maximal independent sets in connected graphs", Journal of Graph Theory 11 (4): 463–470, doi:10.1002/jgt.3190110403.
- ↑ "Sloane's A002478 : Bisection of A000930", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A051894 : Number of monic polynomials with integer coefficients of degree n with all roots in unit disc", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A118312 : Number of squares on infinite chessboard that a knight can reach in n moves from a fixed square", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A046976 : Numerators of Taylor series for sec(x) = 1/cos(x)", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Sloane's A006378 : Prime self (or Colombian) numbers: primes not expressible as the sum of an integer and its digit sum", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Grand Canyon National Park, Frequently Asked Questions, National Park Service, retrieved September 13, 2015