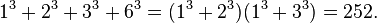252 (number)

← 251 252 253 →
Cardinal two hundred fifty-two
Ordinal 252nd
(two hundred and fifty-second)
Factorization 22× 32× 7
Divisors 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, 252
Roman numeral CCLII
Binary 111111002
Ternary 1001003
Quaternary 33304
Quinary 20025
Senary 11006
Octal 3748
Duodecimal 19012
Hexadecimal FC16
Vigesimal CC20
Base 36 7036

252 (two hundred [and] fifty-two) is the natural number following 251 and preceding 253.

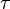252 is the central binomial coefficient \tbinom{10}{5},[1] and is \tau(3), where \tau is the Ramanujan tau function.[2] 252 is also 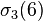\sigma_3(6), where 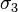\sigma_3 is the function that sums the cubes of the divisors of its argument:[3]

1^3+2^3+3^3+6^3=(1^3+2^3)(1^3+3^3)=252.

It is a practical number,[4] and a hexagonal pyramidal number.[5] There are 252 points on the surface of a cuboctahedron of radius five in the fcc lattice,[6] 252 ways of writing the number 4 as a sum of six squares of integers,[7] 252 ways of choosing four squares from a 4×4 chessboard up to reflections and rotations,[8] and 252 ways of placing four pieces on a Connect Four board.[9]

References

  1. ↑ "Sloane's A000984 : Central binomial coefficients", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  2. ↑ "Sloane's A000594 : Ramanujan's tau function", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  3. ↑ "Sloane's A001158 : sigma_3(n): sum of cubes of divisors of n", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  4. ↑ "Sloane's A005153 : Practical numbers", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  5. ↑ "Sloane's A002412 : Hexagonal pyramidal numbers, or greengrocer's numbers", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  6. ↑ "Sloane's A005901 : Number of points on surface of cuboctahedron", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  7. ↑ "Sloane's A000141 : Number of ways of writing n as a sum of 6 squares", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  8. ↑ "Sloane's A019318 : Number of inequivalent ways of choosing n squares from an n X n board, considering rotations and reflections to be the same", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  9. ↑ "Sloane's A090224 : Number of possible positions for n men on a standard 7 X 6 board of Connect-Four", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.


This article is issued from Wikipedia - version of the Tuesday, January 26, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.