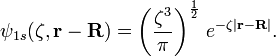1s Slater-type function

A normalized 1s Slater-type function is a function which is used in the descriptions of atoms and in a broader way in the description of atoms in molecules. It is particularly important as the accurate quantum theory description of the smallest free atom, hydrogen. It has the form

\psi_{1s}(\zeta, \mathbf{r - R}) = \left(\frac{\zeta^3}{\pi}\right)^{1 \over 2} \, e^{-\zeta |\mathbf{r - R}|}.

^[1]

It is a particular case of a Slater-type orbital (STO) in which the principal quantum number n is 1. The parameter 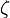$\zeta$ is called the Slater orbital exponent. Related sets of functions can be used to construct STO-nG basis sets which are used in quantum chemistry.

Applications for hydrogen-like atomic systems

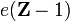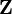A hydrogen-like atom or a hydrogenic atom is an atom with one electron. Except for the hydrogen atom itself (which is neutral) these atoms carry positive charge $e(\mathbf Z-1)$ , where $\mathbf Z$ is the atomic number of the atom. Because hydrogen-like atoms are two-particle systems with an interaction depending only on the distance between the two particles, their (non-relativistic) Schrödinger equation can be exactly solved in analytic form. The solutions are one-electron functions and are referred to as hydrogen-like atomic orbitals.^[2] The electronic Hamiltonian (in atomic units) of a Hydrogenic system is given by
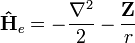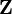$\mathbf{\hat{H}}_e = - \frac{\nabla^2}{2} - \frac{\mathbf Z}{r}$ , where $\mathbf Z$ is the nuclear charge of the hydrogenic atomic system. The 1s electron of a hydrogenic systems can be accurately described by the corresponding Slater orbital:
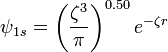$\mathbf \psi_{1s} = \left (\frac{\zeta^3}{\pi} \right ) ^{0.50}e^{-\zeta r}$ , where 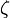$\mathbf \zeta$ is the Slater exponent. This state, the ground state, is the only state that can be described by a Slater orbital. Slater orbitals have no radial nodes, while the excited states of the hydrogen atom have radial nodes.

Exact energy of a hydrogen-like atom

The energy of a hydrogenic system can be exactly calculated analytically as follows :
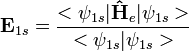$\mathbf E_{1s} = \frac{<\psi_{1s}|\mathbf{\hat{H}}_e|\psi_{1s}>}{<\psi_{1s}|\psi_{1s}>}$ , where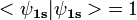 $\mathbf{<\psi_{1s}|\psi_{1s}>} = 1$
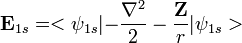
$\mathbf E_{1s} = <\psi_{1s}|\mathbf - \frac{\nabla^2}{2} - \frac{\mathbf Z}{r}|\psi_{1s}>$
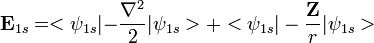
$\mathbf E_{1s} = <\psi_{1s}|\mathbf - \frac{\nabla^2}{2}|\psi_{1s}>+<\psi_{1s}| - \frac{\mathbf Z}{r}|\psi_{1s}>$
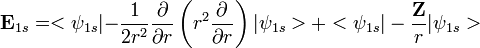$\mathbf E_{1s} = <\psi_{1s}|\mathbf - \frac{1}{2r^2}\frac{\partial}{\partial r}\left (r^2 \frac{\partial}{\partial r}\right )|\psi_{1s}>+<\psi_{1s}| - \frac{\mathbf Z}{r}|\psi_{1s}>$ . Using the expression for Slater orbital, 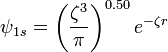$\mathbf \psi_{1s} = \left (\frac{\zeta^3}{\pi} \right ) ^{0.50}e^{-\zeta r}$ the integrals can be exactly solved. Thus,
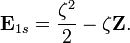
$\mathbf E_{1s} = <\left (\frac{\zeta^3}{\pi} \right ) ^{0.50}e^{-\zeta r}|-\left (\frac{\zeta^3}{\pi} \right )^{0.50}e^{-\zeta r}\left[\frac{-2r\zeta+r^2\zeta^2}{2r^2}\right]>+<\psi_{1s}| - \frac{\mathbf Z}{r}|\psi_{1s}>$ $\mathbf E_{1s} = \frac{\zeta^2}{2}-\zeta \mathbf Z.$

The optimum value for 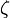$\mathbf \zeta$ is obtained by equating the differential of the energy with respect to 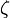$\mathbf \zeta$ as zero.
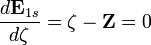$\frac{d\mathbf E_{1s}}{d\zeta}=\zeta-\mathbf Z=0$ . Thus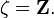 $\mathbf \zeta=\mathbf Z.$

Non relativistic energy

The following energy values are thus calculated by using the expressions for energy and for the Slater exponent.

Hydrogen : H
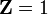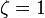
$\mathbf Z=1$ and $\mathbf \zeta=1$
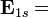$\mathbf E_{1s}=$ −0.5 E_h
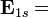$\mathbf E_{1s}=$ −13.60569850 eV
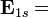$\mathbf E_{1s}=$ −313.75450000 kcal/mol

Gold : Au(78+)
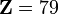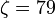
$\mathbf Z=79$ and $\mathbf \zeta=79$
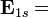$\mathbf E_{1s}=$ −3120.5 E_h
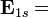$\mathbf E_{1s}=$ −84913.16433850 eV
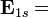$\mathbf E_{1s}=$ −1958141.8345 kcal/mol.

Relativistic energy of Hydrogenic atomic systems

Hydrogenic atomic systems are suitable models to demonstrate the relativistic effects in atomic systems in a simple way. The energy expectation value can calculated by using the Slater orbitals with or without considering the relativistic correction for the Slater exponent 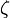$\mathbf \zeta$ . The relativistically corrected Slater exponent 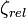$\mathbf \zeta_{rel}$ is given as
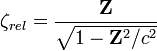$\mathbf \zeta_{rel}= \frac{\mathbf Z}{\sqrt {1-\mathbf Z^2/c^2}}$ .
The relativistic energy of an electron in 1s orbital of a hydrogenic atomic systems is obtained by solving the Dirac equation.
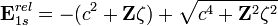$\mathbf E_{1s}^{rel} = -(c^2+\mathbf Z\zeta)+\sqrt{c^4+\mathbf Z^2\zeta^2}$ .
Following table illustrates the relativistic corrections in energy and it can be seen how the relativistic correction scales with the atomic number of the system.

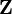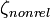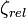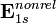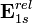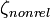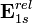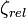Atomic system	$\mathbf Z$	$\mathbf \zeta_{non rel}$	$\mathbf \zeta_{rel}$	$\mathbf E_{1s}^{non rel}$	$\mathbf E_{1s}^{rel}$ using $\mathbf \zeta_{non rel}$	$\mathbf E_{1s}^{rel}$ using $\mathbf \zeta_{rel}$
H	1	1.00000000	1.00002663	−0.50000000 E_h	−0.50000666 E_h	−0.50000666 E_h
				−13.60569850 eV	−13.60587963 eV	−13.60587964 eV
				−313.75450000 kcal/mol	−313.75867685 kcal/mol	−313.75867708 kcal/mol
Au(78+)	79	79.00000000	96.68296596	−3120.50000000 E_h	−3343.96438929 E_h	−3434.58676969 E_h
				−84913.16433850 eV	−90993.94255075 eV	−93459.90412098 eV
				−1958141.83450000 kcal/mol	−2098367.74995699 kcal/mol	−2155234.10926142 kcal/mol

References

↑ Attila Szabo & Neil S. Ostlund (1996). Modern Quantum Chemistry - Introduction to Advanced Electronic Structure Theory. Dover Publications Inc. p. 153. ISBN 0-486-69186-1.
↑ In quantum chemistry an orbital is synonymous with "one-electron function", i.e., a function of x, y, and z.

This article is issued from Wikipedia - version of the Wednesday, December 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.