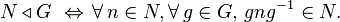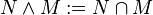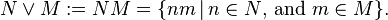Normal subgroup

Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Quotient group (Semi-)direct product Group homomorphisms kernel image direct sum wreath product simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable List of group theory topics Glossary of group theory
Finite groups Classification of finite simple groups cyclic alternating Lie type sporadic Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Symmetric group Sn Klein four-group V Dihedral group Dn Quaternion group Q Dicyclic group Dicn
Discrete groups Lattices Integers (Z) Lattice Modular groups PSL(2,Z) SL(2,Z)
Topological / Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Elliptic curve Linear algebraic group Abelian variety

In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup H of a group G is normal in G if and only if gH = Hg for all g in G, i.e., the sets of left and right cosets coincide.^[1] Normal subgroups (and only normal subgroups) can be used to construct quotient groups from a given group.

Évariste Galois was the first to realize the importance of the existence of normal subgroups.^[2]

Definitions

A subgroup N of a group G is called a normal subgroup if it is invariant under conjugation; that is, for each element n in N and each g in G, the element gng⁻¹ is still in N.^[3] We write

For any subgroup, the following conditions are equivalent to normality. Therefore any one of them may be taken as the definition:

• For all g in G, gNg⁻¹ ⊆ N.
• For all g in G, gNg⁻¹ = N.
• g,h ∈ G, gh ∈ N → hg ∈ N.
• The sets of left and right cosets of N in G coincide.
• For all g in G, gN = Ng.
• For all x,y,g,h ∈ G, x ∈ Ng and y ∈ Nh → xy ∈ N(gh).
• N is a union of conjugacy classes of G.
• There is some homomorphism on G for which N is the kernel.

The last condition accounts for some of the importance of normal subgroups; they are a way to internally classify all homomorphisms defined on a group. For example, a non-identity finite group is simple if and only if it is isomorphic to all of its non-identity homomorphic images,^[4] a finite group is perfect if and only if it has no normal subgroups of prime index, and a group is imperfect if and only if the derived subgroup is not supplemented by any proper normal subgroup.

Examples

• The subgroup {e} consisting of just the identity element of G and G itself are always normal subgroups of G. The former is called the trivial subgroup, and if these are the only normal subgroups, then G is said to be simple.
• The center of a group is a normal subgroup.
• The commutator subgroup is a normal subgroup.
• More generally, any characteristic subgroup is normal, since conjugation is always an automorphism.
• All subgroups N of an abelian group G are normal, because gN = Ng. A group that is not abelian but for which every subgroup is normal is called a Hamiltonian group.
• The translation group in any dimension is a normal subgroup of the Euclidean group (with the orthogonal group as the quotient group); for example in 3D rotating, translating, and rotating back results in only translation; also reflecting, translating, and reflecting again results in only translation (a translation seen in a mirror looks like a translation, with a reflected translation vector). The translations by a given distance in any direction form a conjugacy class; the translation group is the union of those for all distances.
• In the Rubik's Cube group, the subgroup consisting of operations which only affect the corner pieces is normal, because no conjugate transformation can make such an operation affect an edge piece instead of a corner. By contrast, the subgroup consisting of turns of the top face only is not normal, because a conjugate transformation can move parts of the top face to the bottom and hence not all conjugates of elements of this subgroup are contained in the subgroup.

Properties

• Normality is preserved upon surjective homomorphisms, and is also preserved upon taking inverse images.
• Normality is preserved on taking direct products.
• If H is a normal subgroup of G, and K is a subgroup of G containing H, then H is a normal subgroup of K.
• A normal subgroup of a normal subgroup of a group need not be normal in the group. That is, normality is not a transitive relation. The smallest group exhibiting this phenomenon is the dihedral group of order 8. However, a characteristic subgroup of a normal subgroup is normal. Also, a normal subgroup of a central factor is normal. In particular, a normal subgroup of a direct factor is normal. A group in which normality is transitive is called a T-group.
• Every subgroup of index 2 is normal. More generally, a subgroup H of finite index n in G contains a subgroup K normal in G and of index dividing n! called the normal core. In particular, if p is the smallest prime dividing the order of G, then every subgroup of index p is normal.

Lattice of normal subgroups

The normal subgroups of a group G form a lattice under subset inclusion with least element {e} and greatest element G. Given two normal subgroups N and M in G, meet is defined as

and join is defined as

The lattice is complete and modular.

Normal subgroups and homomorphisms

If N is normal subgroup, we can define a multiplication on cosets by

(a₁N)(a₂N) := (a₁a₂)N.

This turns the set of cosets into a group called the quotient group G/N. There is a natural homomorphism f: G → G/N given by f(a) = aN. The image f(N) consists only of the identity element of G/N, the coset eN = N.

In general, a group homomorphism f: G → H sends subgroups of G to subgroups of H. Also, the preimage of any subgroup of H is a subgroup of G. We call the preimage of the trivial group {e} in H the kernel of the homomorphism and denote it by ker(f). As it turns out, the kernel is always normal and the image f(G) of G is always isomorphic to G/ker(f) (the first isomorphism theorem). In fact, this correspondence is a bijection between the set of all quotient groups G/N of G and the set of all homomorphic images of G (up to isomorphism). It is also easy to see that the kernel of the quotient map, f: G → G/N, is N itself, so we have shown that the normal subgroups are precisely the kernels of homomorphisms with domain G.

See also

References

Further reading

• I. N. Herstein, Topics in algebra. Second edition. Xerox College Publishing, Lexington, Mass.-Toronto, Ont., 1975. xi+388 pp.

External links

• Weisstein, Eric W., "normal subgroup", MathWorld.
• Normal subgroup in Springer's Encyclopedia of Mathematics
• Robert Ash: Group Fundamentals in Abstract Algebra. The Basic Graduate Year
• Timothy Gowers, Normal subgroups and quotient groups
• John Baez, What's a Normal Subgroup?