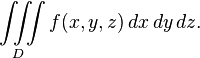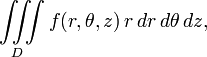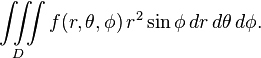Volume integral

In mathematics—in particular, in multivariable calculus—a volume integral refers to an integral over a 3-dimensional domain, that is, it is a special case of multiple integrals. Volume integrals are especially important in physics for many applications, for example, to calculate flux densities.

In coordinates

It can also mean a triple integral within a region D in R3 of a function 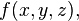f(x,y,z), and is usually written as:

\iiint\limits_D f(x,y,z)\,dx\,dy\,dz.

A volume integral in cylindrical coordinates is

\iiint\limits_D f(r,\theta,z)\,r\,dr\,d\theta\,dz,
Volume element in spherical coordinates

and a volume integral in spherical coordinates (using the convention for angles with \theta as the azimuth and \phi measured from the polar axis (see more on conventions)) has the form

\iiint\limits_D f(r,\theta,\phi)\,r^2 \sin\phi \,dr \,d\theta\, d\phi .

Example 1

Integrating the function 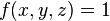f(x,y,z) = 1 over a unit cube yields the following result:

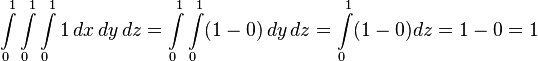
\int\limits_0^1\int\limits_0^1\int\limits_0^1 1 \,dx\, dy \,dz = \int\limits_0^1\int\limits_0^1 (1 - 0) \,dy \,dz = \int\limits_0^1 (1 - 0) dz = 1 - 0 = 1

So the volume of the unit cube is 1 as expected. This is rather trivial however, and a volume integral is far more powerful. For instance if we have a scalar function 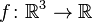\begin{align} f\colon \mathbb{R}^3 &\to \mathbb{R} \end{align} describing the density of the cube at a given point (x,y,z) by f = x+y+z then performing the volume integral will give the total mass of the cube:

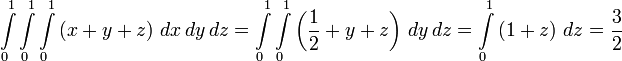
\int\limits_0^1\int\limits_0^1\int\limits_0^1 \left(x + y + z\right) \, dx \,dy \,dz = \int\limits_0^1\int\limits_0^1 \left(\frac 12 + y + z\right) \, dy \,dz = \int \limits_0^1 \left(1 + z\right) \, dz = \frac 32

See also

External links

This article is issued from Wikipedia - version of the Monday, September 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.