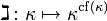Gimel function

In axiomatic set theory, the gimel function is the following function mapping cardinal numbers to cardinal numbers:

\gimel \colon \kappa \mapsto \kappa ^{\mathrm {cf} (\kappa )}

where cf denotes the cofinality function; the gimel function is used for studying the continuum function and the cardinal exponentiation function. The symbol 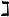$\gimel$ is a serif form of the Hebrew letter gimel.

The gimel hypothesis states that 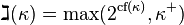$\gimel (\kappa )=\max(2^{{\text{cf}}(\kappa )},\kappa ^{+})$

Values of the Gimel function

The gimel function has the property 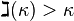$\gimel (\kappa )>\kappa$ for all infinite cardinals κ by König's theorem.

For regular cardinals 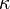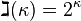$\kappa$ , $\gimel (\kappa )=2^{\kappa }$ , and Easton's theorem says we don't know much about the values of this function. For singular 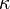$\kappa$ , upper bounds for 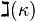$\gimel (\kappa )$ can be found from Shelah's PCF theory.

Reducing the exponentiation function to the gimel function

Bukovský (1965) showed that all cardinal exponentiation is determined (recursively) by the gimel function as follows.

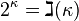
If κ is an infinite regular cardinal (in particular any infinite successor) then $2^{\kappa }=\gimel (\kappa )$
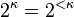
If κ is infinite and singular and the continuum function is eventually constant below κ then $2^{\kappa }=2^{<\kappa }$
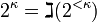
If κ is a limit and the continuum function is not eventually constant below κ then $2^{\kappa }=\gimel (2^{<\kappa })$

The remaining rules hold whenever κ and λ are both infinite:

If ℵ₀≤κ≤λ then κ^λ = 2^λ
If μ^λ≥κ for some μ<κ then κ^λ = μ^λ
If κ> λ and μ^λ<κ for all μ<κ and cf(κ)≤λ then κ^λ = κ^cf(κ)
If κ> λ and μ^λ<κ for all μ<κ and cf(κ)>λ then κ^λ = κ

References

Bukovský, L. (1965), "The continuum problem and powers of alephs", Comment. Math. Univ. Carolinae 6: 181–197, MR 0183649
Jech, Thomas J. (1973), "Properties of the gimel function and a classification of singular cardinals" (PDF), Fund. Math., Collection of articles dedicated to Andrzej Mostowski on the occasion of his sixtieth birthday, I. 81 (1): 57–64, MR 0389593
Thomas Jech, Set Theory, 3rd millennium ed., 2003, Springer Monographs in Mathematics, Springer, ISBN 3-540-44085-2.

This article is issued from Wikipedia - version of the Tuesday, December 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.