Limit point
In mathematics, a limit point of a set S in a topological space X is a point x (which is in X, but not necessarily in S) that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S. This concept profitably generalizes the notion of a limit and is the underpinning of concepts such as closed set and topological closure. Indeed, a set is closed if and only if it contains all of its limit points, and the topological closure operation can be thought of as an operation that enriches a set by uniting it with its limit points.
Definition
Let S be a subset of a topological space X. A point x in X is a limit point of S if every neighbourhood of x contains at least one point of S different from x itself. Note that it doesn't make a difference if we restrict the condition to open neighbourhoods only.
This is equivalent, in a T1 space, to requiring that every neighbourhood of x contains infinitely many points of S. It is often convenient to use the "open neighbourhood" form of the definition to show that a point is a limit point and to use the "general neighbourhood" form of the definition to derive facts from a known limit point.
Alternatively, if the space X is sequential, we may say that x ∈ X is a limit point of S if and only if there is an ω-sequence of points in S \ {x} whose limit is x; hence, x is called a limit point.
Types of limit points
 A sequence enumerating all positive rational numbers. Each positive real number is a cluster point. |
| With respect to the usual Euclidean topology, the sequence of rational numbers xn = (-1)n·n/n+1 has no limit (i.e. does not converge), but has two accumulation points (which are considered limit points here), viz. -1 and +1. |
If every open set containing x contains infinitely many points of S then x is a specific type of limit point called an ω-accumulation point of S.
If every open set containing x contains uncountably many points of S then x is a specific type of limit point called a condensation point of S.
If every open set U containing x satisfies |U ∩ S| = |S| then x is a specific type of limit point called a complete accumulation point of S.
A point x ∈ X is a cluster point or accumulation point of a sequence (xn)n ∈ N if, for every neighbourhood V of x, there are infinitely many natural numbers n such that xn ∈ V. If the space is Fréchet–Urysohn, this is equivalent to the assertion that x is a limit of some subsequence of the sequence (xn)n ∈ N. The set of all cluster points of a sequence is sometimes called a limit set.
The concept of a net generalizes the idea of a sequence. Let 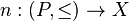 be a net, where
be a net, where  is a directed set. The point
is a directed set. The point 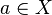 is said to be a cluster point of the net
is said to be a cluster point of the net  if for any neighborhood
if for any neighborhood 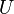 of
of  and any
and any  , there is some
, there is some 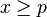 such that
such that 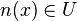 , equivalently, if
, equivalently, if  has a subnet which converges to
has a subnet which converges to  . Cluster points in nets encompass the idea of both condensation points and ω-accumulation points. Clustering and limit points are also defined for the related topic of filters.
. Cluster points in nets encompass the idea of both condensation points and ω-accumulation points. Clustering and limit points are also defined for the related topic of filters.
Some facts
- We have the following characterisation of limit points: x is a limit point of S if and only if it is in the closure of S \ {x}.
- Proof: We use the fact that a point is in the closure of a set if and only if every neighbourhood of the point meets the set. Now, x is a limit point of S, if and only if every neighbourhood of x contains a point of S other than x, if and only if every neighbourhood of x contains a point of S \ {x}, if and only if x is in the closure of S \ {x}.
- If we use L(S) to denote the set of limit points of S, then we have the following characterisation of the closure of S: The closure of S is equal to the union of S and L(S). [This fact appears to be just the definition, as stated in the closure. It might become less trivial, if other definition of closure is used.]
- Proof: ("Left subset") Suppose x is in the closure of S. If x is in S, we are done. If x is not in S, then every neighbourhood of x contains a point of S, and this point cannot be x. In other words, x is a limit point of S and x is in L(S). ("Right subset") If x is in S, then every neighbourhood of x clearly meets S, so x is in the closure of S. If x is in L(S), then every neighbourhood of x contains a point of S (other than x), so x is again in the closure of S. This completes the proof.
- A corollary of this result gives us a characterisation of closed sets: A set S is closed if and only if it contains all of its limit points.
- Proof: S is closed if and only if S is equal to its closure if and only if S = S ∪ L(S) if and only if L(S) is contained in S.
- Another proof: Let S be a closed set and x a limit point of S. If x is not in S, then we can find an open set around x contained entirely in the complement of S. But then this set contains no point in S, so x is not a limit point, which contradicts our original assumption. Conversely, assume S contains all its limit points. We shall show that the complement of S is an open set. Let x be a point in the complement of S. By assumption, x is not a limit point, and hence there exists an open neighborhood U of x that does not intersect S, and so U lies entirely in the complement of S. Since this argument holds for arbitrary x in the complement of S, the complement of S can be expressed as a union of open neighborhoods of the points in the complement of S. Hence the complement of S is open.
- No isolated point is a limit point of any set.
- Proof: If x is an isolated point, then {x} is a neighbourhood of x that contains no points other than x.
- A space X is discrete if and only if no subset of X has a limit point.
- Proof: If X is discrete, then every point is isolated and cannot be a limit point of any set. Conversely, if X is not discrete, then there is a singleton {x} that is not open. Hence, every open neighbourhood of {x} contains a point y ≠ x, and so x is a limit point of X.
- If a space X has the trivial topology and S is a subset of X with more than one element, then all elements of X are limit points of S. If S is a singleton, then every point of X \ S is still a limit point of S.
- Proof: As long as S \ {x} is nonempty, its closure will be X. It's only empty when S is empty or x is the unique element of S.
- By definition, every limit point is an adherent point.
References
- Hazewinkel, Michiel, ed. (2001), "Limit point of a set", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4