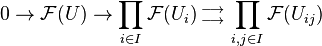Étale topos

In mathematics, the étale topos of a scheme X is the category of all étale sheaves on X. An étale sheaf is a sheaf on the étale site of X.

Definition

Let X be a scheme. An étale covering of X is a family 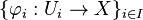$\{ \varphi_i: U_i \to X \}_{i\in I}$ , where each $\varphi_i$ is an étale morphism of schemes, such that the family is jointly surjective that is $X = \bigcup_{i \in I} \varphi_i(U_i)$ .

The category Ét(X) is the category of all étale schemes over X. The collection of all étale coverings of a étale scheme U over X i.e. an object in Ét(X) defines a Grothendieck pretopology on Ét(X) which in turn induces a Grothendieck topology, the étale topology on X. The category together with the étale topology on it is called the étale site on X.

The étale topos 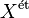$X^\text{ét}$ of a scheme X is then the category of all sheaves of sets on the site Ét(X). Such sheaves are called étale sheaves on X. In other words, an étale sheaf 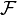$\mathcal F$ is a (contravariant) functor from the category Ét(X) to the category of sets satisfying the following sheaf axiom:

For each étale U over X and each étale covering 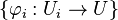$\{ \varphi_i: U_i \to U \}$ of U the sequence

0 \to \mathcal F(U) \to \prod_{i \in I} \mathcal F(U_i) {{{} \atop \longrightarrow}\atop{\longrightarrow \atop {}}} \prod_{i,j \in I} \mathcal F(U_{ij})

is exact, where 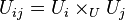$U_{ij} = U_i \times_U U_j$ .

This article is issued from Wikipedia - version of the Wednesday, November 19, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.